ECS289K Project A

• Brief summary

  Optimize/tune sequential code for square matrix multiply (aka dgemm: C = C + A B where A, B, and C have dimension m by m) on a machine of your choice. Explain the optimizations you use and the performance characteristics (e.g. cache sizes, latencies). What happens when you run the code on a different machine? Why?

• Overview

  Matrix multiplication is a basic building block in many scientific computations; and since it is an O(n³) algorithm, these codes often spend much of their time in matrix multiplication. The most naive code to multiply matrices is short, sweet, simple, and very slow:

  for i = 1 to m
      for j = 1 to m
        for k = 1 to m
          C(i,j) = C(i,j) + A(i,k) * B(k,j)
        end
      end
  end 
  

  We're providing implementations of the trivial unoptimized matrix multiply code in C and Fortran, and a very simple blocked implementation in C. We're also providing a wrapper for the BLAS (Basic Linear Algebra Subroutines) library. The BLAS is a standard interface for building blocks like matrix multiplication, and many vendors provide optimized versions of the BLAS for their platforms. You may want to compare your routines to codes that others have optimized; if you do, think about the relative difficulty of using someone else's library to writing and optimizing your own routine. Knowing when and how to make use of standard libraries is an important skill in building fast programs!

  The unblocked routines we provide do as poorly as you'd expect, and the blocked routine provided doesn't do much better.

  

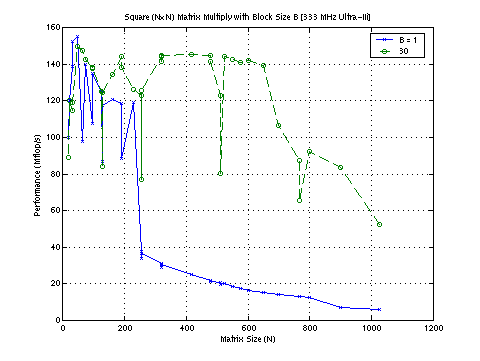
  The performance of the two routines is shown above. The naive unblocked routine is the "B=1" curve, and is just the standard three nested loops. The blocked code (block size of 30, selected as the "best" in an exhaustive search of square tile sizes up to B=256) is shown in green. The peak performance of the machine used is 667 MFlop/s, and both implementations achieve less than a quarter of that performance. However, the unblocked routine's performance completely dies on matrices larger than 255 x 255, while the blocked routine gives more consistent performance for all the tested sizes. Note the performance dips at powers of 2 (cache conflicts). The machine used for this diagram has a 2 Mbyte external cache, and 3 matrices * 256x256 entries * 8 bytes/entry is 1.5 Mbytes. Obviously, there's overhead in both operation count and memory usage.

• Details

  The code is distributed in tar format and directly.
  (a new makefile ``Makefile2'', which doesn't require to use ``gexec'')

  You need to write a dgemm.c that contains a function with the following C signature:

        void
        square_dgemm (const unsigned M, 
                      const double *A, const double *B, double *C)
  

  If you would prefer, you can also write a Fortran function in a file fdgemm.f:

          subroutine sdgemm(M, A, B, C)
  c
  c       .. Parameters ..
          integer M
          double precision A(M,M)
          double precision B(M,M)
          double precision C(M,M)
  

  Note that the matrices are stored in column-major order. Also, your program will actually be doing a multiply and add operation:

      C := C + A*B
  

  You will get a lot of improvement from blocking/tiling, but you may want to play with other optimizations doing some independent reading (see references).

• Submission

  Create a webpage on the project to include the followings:

  • the optimizations used or attempted,
  • the results of those optimizations,
  • try to the reason for any odd behavior (e.g., dips) in performance, and how the same kernel performs on a different hardware platform.
  • To show the results of your optimizations, include a graph comparing your dgemm.c with the included basic_dgemm.c. Try to explain why it performs poorly. Your explanations should rely heavily on knowledge of the memory hierarchy.

• References

  • The optimizations used in PHiPAC and ATLAS may be interesting. Note: You cannot use PHiPAC or ATLAS to generate your matrix multiplication kernels. You can write your own code generator, however. You might want to read the tech report (.ps.gz) on PHiPAC. The section on C coding guidelines will be particuarly relevant.
  • There is a classic paper (.ps) on the idea of cache blocking in the context of matrix multiply by Monica Lam, et al.
  • The software performance tuning project at Berkeley BeBOP
  • Need information on gcc compiler flags? Read the manual.

• Thanks

  To David Bindel and David Garmire in setting up this assigment.