ECS 120 Theory of Computation

Equivalence of Regular Expressions and NFAs

Julian Panetta

University of California, Davis

Equivalence of regex’s and NFAs

NFAs and DFAs have equivalent computational power.
Regular grammars and DFAs have equivalent computational power.

Today:
- Prove that NFAs and regex’s have equivalent computational power.
  Strategy: induction proofs that incrementally simplify the regex/NFA.
- Conclude that the following classes of languages are actually all the same:
  - DFA-decidable
  - NFA-decidable
  - regex-decidable
  - RG-decidable
- Languages of this class are called regular languages.

Implementing regex’s with NFAs

Theorem: Any regex-decidable language is NFA-decidable.

Proof

Recall the formal definition:

\(R\) is a regular expression deciding language \(L(R) \subseteq \Sigma^*\) if one of the following holds:

(base) \(R = a\) for some \(a \in \Sigma\). Then \(L(R) = \{a\}\).
(base) \(R = \emptystring\). Then \(L(R) = \{\emptystring\}\).
(base) \(R = \emptyset\). Then \(L(R) = \{\}\).
(inductive) \(R = (R_1) \cup (R_2)\) for regex’s \(R_1, R_2\). Then \(L(R) = L(R_1) \cup L(R_2)\).
(inductive) \(R = (R_1)(R_2)\) for regex’s \(R_1, R_2\). Then \(L(R) = L(R_1) \circ L(R_2)\).
(inductive) \(R = (R_1)^*\) for a regex \(R_1\). Then \(L(R) = L(R_1)^*\).

This inductive definition implies a “tree structure” that we can exploit to construct an NFA!

Implementing regex’s with NFAs

Theorem: Any regex-decidable language is NFA-decidable.

Proof

Inductive proof:

For any regular expression \(R\), we can construct an NFA \(N\) such that \(L(N) = L(R)\).

The base cases of the inductive definition are the base cases of the proof!

If \(R = a\) for some \(a \in \Sigma\), then \(L(R) = \{a\}\) decided by the NFA
If \(R = \emptystring\), then \(L(R) = \{\emptystring\}\) decided by the NFA
If \(R = \emptyset\), then \(L(R) = \{\}\) decided by the NFA

Implementing regex’s with NFAs

Theorem: Any regex-decidable language is NFA-decidable.

Proof

Inductive proof:

For any regular expression \(R\), we can construct an NFA \(N\) such that \(L(N) = L(R)\).

The recursive cases of the definition are the inductive steps of the proof!

If \(R = (R_1) \cup (R_2)\) for \(R_1, R_2\) regexes, then \(L(R) = L(R_1) \cup L(R_2)\).

\(L(R_1)\) and \(L(R_2)\) are both NFA-decidable by the inductive hypothesis.
By closure under union, so is \(L(R) = L(R_1) \cup L(R_2)\)!
If \(R = (R_1)(R_2)\) for \(R_1, R_2\) regexes, then \(L(R) = L(R_1) \circ L(R_2)\).

\(L(R_1)\) and \(L(R_2)\) are both NFA-decidable by the inductive hypothesis.
By closure under concatenation, so is \(L(R) = L(R_1) \circ L(R_2)\)!
If \(R = (R_1)^*\) for \(R_1\) a regex, then \(L(R) = L(R_1)^*\).

\(L(R_1)\)is NFA-decidable by the inductive hypothesis.
By closure under Kleene star, so is \(L(R) = L(R_1)^*\)!

This completes the proof!

Implementing regex’s with NFAs example: \(\string{(a \cup ab)^* b}\)

\(\stackrel{\Large \nwarrow}{\large \leftarrow}\) base cases
Don’t bother optimizing by collapsing two states between \(\varepsilon\)-transition. (unsafe in general, even if it happens to work here)

Converting NFAs to regex’s

Theorem: Any NFA-decidable language is regex-decidable.

Starting point: “Expression Automata” (or “Generalized NFAs” in Sipser)

Label the transition arrows of an NFA with regular expressions that match substrings of the input rather than individual symbols.

data/images/regex_nfa/expression_automaton.svg

❌ \(\emptystring\)
❌ \(\string{a}\)
❌ \(\string{b}\)

✅ \(\string{ba}\)
✅ \(\string{bba}\)
✅ \(\string{baa}\)

❌ \(\string{baaba}\)
✅ \(\string{baababa}\)
✅ \(\string{baababa}\)

✅ \(\string{bbaaababbba}\)
❌ \(\string{bbaabab}\)
❌ \(\string{bbaababab}\)

Converting NFAs to Regexes

Theorem: Any NFA-decidable language is regex-decidable.

Starting point: “Expression Automata” (or “Generalized NFAs” in Sipser)

Label the transition arrows of an NFA with regular expressions that match substrings of the input rather than individual symbols.

Proof idea:

Any NFA \(N\) is already a valid expression automaton.
Incrementally convert \(N\) into a simpler equivalent expression automaton \(E\) of the form:

where \(R\) is a regular expression.

Then \(L(N) = L(E) = L(R)\)!

Converting NFAs to regex’s: First step

In our first step, we modify \(N\) so that:

The start state has no inbound transitions.
There is a single accept state with no outbound transitions.

Given \(N = (Q, \Sigma, \Delta, q_0, F)\),
construct \(N' = (Q', \Sigma, \Delta', s, F')\):

\(Q' = Q \cup \{s, a\}\) where \(s, a \notin Q\)
\(F' = \{a\}\)
Assuming \(\Delta\) represents a
set of transitions: \(\Delta' = \Delta \cup \{(s, \emptystring, q_0)\} \cup \setbuild{(q, \emptystring, a)}{q \in F}\)

\(L(N') = L(N)\) because:
There exists a computation sequence of \(N\) \(r_1, r_2, \ldots, r_n\) that accepts \(w\) if and only if \(s, r_1, r_2, \ldots, r_n, a\) is a computation sequence of \(N'\) accepting \(w\).

Converting NFAs to Regexes: Incremental Simplification

We then apply incremental simplifications that remove the states “in the box” one by one:

data/images/regex_nfa/generic_n_third_step.svg

data/images/regex_nfa/generic_n_fourth_step.svg

How does this work in general?

Converting NFAs to Regexes: Incremental Simplification

The final simplification step operates on an EA that looks like:
We can rip state “i” out of the diagram but still accept strings whose computational sequences through it by changing the connection between \(s\) and \(a\):
Both EAs accept exactly strings of the form
- \(w \in L(W)\), or
- \(x y^k z\) for some \(k \in \N\) where \(x \in L(X), y \in L(Y)\), and \(z \in L(Z)\).

Converting NFAs to Regexes: Incremental Simplification

When more than three states remain:

Select any state other than \(s\) or \(a\) and call it \(i\).
Iterate over pairs of states \(q\) and \(r\) with transitions \(q \stackrel{a}{\to} i\) and \(i \stackrel{b}{\to} r\) (even if \(q = r\))
For each of these pairs, transform:
into:
Repeat until only 2 states remain!

Example removing state \(i\)

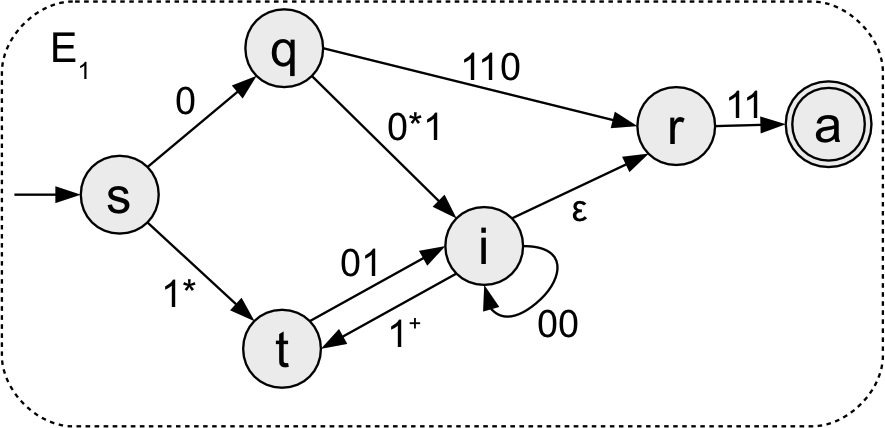
data/images/regex_nfa/example_conversion.png

How to get from \(q\) to \(t\) going through \(i\)? \(0^*1\) (go from \(q\) to \(i\)) \((00)^*\) (loop on \(i\)) \(1^+\) (go from \(i\) to \(t\))
- add new transition \(q \stackrel{0^*1 (00)^* 1^+}{\to} t\)
How to get from \(q\) to \(r\) going through \(i\)? \(\fragment{0^*1} \fragment{(00)^*} \fragment{\emptystring} \fragment{= 0^*1 (00)^*}\) OR directly follow \(q \stackrel{110}{\to} r\).
- replace existing \(q \stackrel{110}{\to} r\) transition with \(q \stackrel{0^*1(00)^* \cup 110}{\to} r\)
How to get from \(t\) to \(r\) going through \(i\)? \(\fragment{01 (00)^*}\)
- add new transition: \(t \stackrel{01(00)^*}{\to} r\)
How to get from \(t\) to \(t\) going through \(i\)? \(\fragment{01 (00)^* 1^+}\)
- add new self-transition: \(t \stackrel{01(00)^*1^+}{\to} t\)

data/images/regex_nfa/ch6-ea-remove-state-after.svg

Example conversion (Sipser, Figure 1.69)

Title

Equivalence of regex’s and NFAs

Implementing regex’s with NFAs

Implementing regex’s with NFAs

Implementing regex’s with NFAs

Implementing regex’s with NFAs example: \(\string{(a \cup ab)^* b}\)

Converting NFAs to regex’s

Converting NFAs to Regexes

Converting NFAs to regex’s: First step

Converting NFAs to Regexes: Incremental Simplification

Converting NFAs to Regexes: Incremental Simplification

Converting NFAs to Regexes: Incremental Simplification

Example removing state \(i\)

Example conversion (Sipser, Figure 1.69)