Title
Recall: Formal Definition of a Turing Machine
Recall: A Turing machine (TM) is a 7-tuple: \(M = (Q, \Sigma, \Gamma, \delta, s, q_a, q_r)\) where:

- \(Q\) is a finite set of states.
- \(\Sigma\) is a finite set of input symbols (the input alphabet).
- \(\Gamma\) is a finite set of tape symbols (the tape alphabet) with:
\(\Sigma \subsetneq \Gamma\) and blank symbol ⎵ \(\in \Gamma \setminus \Sigma\). - \(s \in Q\) is the start state.
- \(q_a \in Q\) is the accept state.
- \(q_r \in Q\) is the reject state, where \(q_r \ne q_a\).
- \(\delta: (Q \setminus \{q_a, q_r\}) \times \Gamma \to Q \times \Gamma \times \{L, R, S\}\) is the transition function
\(L\) = move left, \(R\) = move right, \(S\) = stay in place.
Formal Definition of Computation for Turing Machines
How can we describe the “full state” that a Turing machine is in (including its tape)?

A configuration of a TM \(M = (Q, \Sigma, \Gamma, \delta, s, q_a, q_r)\) is a triple: \(C = (q, p, w)\) where:
- \(q \in Q\) is the current state of the TM.
- \(p \in \N^+\) is the tape head position.
- \(w \in \Gamma^\infty\) is a one-way infinite sequence holding the tape content
Sipser uses a different notation “\(u\, q\, v\)” where \(w=uv\) and \(p = |u| + 1\).
Example: \(1011q_70111\).
See Optional Section 8.4 for a definition (uglier) using a finite, growable tape.
Formal Definition of Computation for Turing Machines

A configuration of a TM \(M = (Q, \Sigma, \Gamma, \delta, s, q_a, q_r)\) is a triple: \(C = (q, p, w)\) where:
- \(q \in Q\) is the current state of the TM.
- \(p \in \N^+\) is the tape head position.
- \(w \in \Gamma^\infty\) is a one-way infinite sequence holding the tape content
We define computation by formally specifying how one configuration \(C = (q, p, w)\) transitions to the next configuration \(C' = (q', p', w')\).
We say \(C\) yields \(C'\) (writing \(C \to C'\)) when \(M\) can legally go from \(C\) to \(C'\) in one step: \[ \delta(q, w[p]) = (\fragment{q'}, \fragment{w'[p]}, \fragment{m}) \hspace{5em} \]
We identify moves \(m \in \{L, R, S\}\) with offsets \(\{-1, +1, 0\}\) added to \(p\).
- \(p' = \max(1, p + m)\)
(Move tape head according to \(m\) but don’t go off the left end.) - \(w[i] = w'[i]\) for all \(i \ne p\)
(Leave all other tape cells unchanged.)
- \(p' = \max(1, p + m)\)
Formal Definition of Computation for Turing Machines

A configuration of a TM \(M = (Q, \Sigma, \Gamma, \delta, s, q_a, q_r)\) is a triple: \(C = (q, p, w)\) where:
- \(q \in Q\) is the current state of the TM.
- \(p \in \N^+\) is the tape head position.
- \(w \in \Gamma^\infty\) is a one-way infinite sequence holding the tape content
A configuration \((q, p, w)\) is called:
accepting if \(q = q_a\), rejecting if \(q = q_r\), halting if \(q \in \{q_a, q_r\}\).\(M\) accepts/rejects input \(w \in \Sigma^*\) if there is a finite sequence of configurations \(C_1, C_2, \ldots, C_k\) such that:
- \(C_1 = (\fragment{s}, \fragment{1}, \fragment{w \string{⎵}^\infty})\)
- \(C_i \to C_{i+1}\) for all \(1 \leq i < k\)
- \(C_k\) is accepting/rejecting
If \(M\) neither accepts nor rejects \(w\), we say \(M\) loops (does not halt) on \(w\).
- Three possible outcomes: accept, reject, or loop!
- Defining the languages “recognized” or “decided” by a TM requires more care than with FAs or CFGs.
Languages Recognized/Decided by a Turing Machine
The set of strings that \(M\) accepts is called the language recognized by \(M\), denoted \[L(M) = \{ w \in \Sigma^* \mid M \text{ accepts } w \}\]
A language \(A\) is called Turing-recognizable (or Turing-acceptable, recursively enumerable, or
computably enumerable) if some Turing machine \(M\) recognizes it (\(L(M) = A\)).
True or false: \(w \not \in L(M)\) means that Turing machine \(M\) rejects \(w\).
- True
- False
\(w \not \in L(M)\) means that \(M\) rejects \(w\) or loops on \(w\).
Languages Recognized/Decided by a Turing Machine
The set of strings that \(M\) accepts is called the language recognized by \(M\), denoted \[L(M) = \{ w \in \Sigma^* \mid M \text{ accepts } w \}\]
A language \(A\) is called Turing-recognizable (or Turing-acceptable, recursively enumerable, or
computably enumerable) if some Turing machine \(M\) recognizes it (\(L(M) = A\)).
Claim: Turing-recognizable languages are closed under complement because for any \(M\), we can swap the accept and reject states to form \(M'\) such that \(L(M') = \overline{L(M)}\).
- Correct
- Incorrect
If \(M\) loops on \(w\) then so does \(M'\).
So \(w \notin L(M)\) and \(w \notin L(M')\).
Thus \(L(M') \ne \overline{L(M)}\).
Turing-recognizable languages turn out not to be closed under complement!
Languages Recognized/Decided by a Turing Machine
The set of strings that \(M\) accepts is called the language recognized by \(M\), denoted \[L(M) = \{ w \in \Sigma^* \mid M \text{ accepts } w \}\]
A language \(A\) is called Turing-recognizable (or Turing-acceptable, recursively enumerable, or
computably enumerable) if some Turing machine \(M\) recognizes it (\(L(M) = A\)).
A language \(A\) is called co-Turing-recognizable if its complement is Turing-recognizable.
(If \(A = \overline{L(M)}\) for some Turing machine \(M\)).
- Turing machines that loop forever on certain inputs are not helpful for solving problems!
- A TM that halts on every input is called total.
- A total TM \(M\) such that \(L(M) = A\) is said to decide \(A\) (\(M\) is a decider).
Languages Recognized/Decided by a Turing Machine
The set of strings that \(M\) accepts is called the language recognized by \(M\), denoted \[L(M) = \{ w \in \Sigma^* \mid M \text{ accepts } w \}\]
A language \(A\) is called Turing-recognizable (or Turing-acceptable, recursively enumerable, or
computably enumerable) if some Turing machine \(M\) recognizes it (\(L(M) = A\)).
A language \(A\) is called co-Turing-recognizable if its complement is Turing-recognizable.
(If \(A = \overline{L(M)}\) for some Turing machine \(M\)).
A language \(A\) is called Turing-decidable if there exists a total Turing machine \(M\) (a decider) such that \(L(M) = A\). In other words \(M\) accepts all \(w \in A\) and rejects all \(w \notin A\).
A language is Turing-decidable if and only if it is both Turing-recognizable and co-Turing-recognizable.
Why define \(L(M)\) as the language “recognized” by \(M\) and not “decided” if deciders are more useful?
Mostly mathematical convenience/completeness: \(L(M)\) exists for all Turing machines, even if not total.
Computational Power Review
Any CFG-decidable language is also Turing-decidable.
- True
- False
Proof: The simulator decides all context-free languages (using the Earley parsing algorithm.)
Computational Power Review
Any Turing-decidable language is also CFG-decidable.
- True
- False
Counterexample: \(\setbuild{0^n 1^n 2^n}{n \in \mathbb{N}}\)
import re
def decide(x):
return re.match(r'^0*1*2*$', x) and x.count('0') == x.count('1') == x.count('2')Variants of Turing Machines
- There are many different ways we could define Turing machines without changing which languages are Turing-recognizable.
- For example, Sipser defines the tape head moves as \(\{L, R\}\) instead of \(\{L, R, S\}\).
- We summarize this by saying the definition is robust (not sensitive to changes), explaining its ability to model anything a computer can do.
- Let’s consider how we might relieve the apparent limitation of a single sequential tape:
- Use multiple tapes (one for input and the other for scratch space).
- Use a two-way infinite tape (instead of one-way infinite).
- Use multiple tape heads on a single tape.
- Use a “2D tape” (i.e., an unbounded grid of cells in the 2D plane), a model of “scratch paper”.
- Use random-access memory (allow \(M\) read/write access to an auxiliary “address tape;” teleport the main tape head to addresses as they are read).
- All of these appear more powerful than a single tape Turing machine, but aren’t.
- How do we prove this? Simulate them on a standard TM!
Multitape Turing Machines

- A multitape Turing machine is an ordinary Turing machine but with \(k\) tapes.
Each tape has its own independent read/write head.
The input is loaded onto the first tape, and the other tapes start blank.
Its transition function has the signature: \[ \delta: \fragment{(Q \setminus \{q_a, q_r\}) \times} \fragment{\Gamma^k} \to \fragment{Q} \fragment{\times \Gamma^k} \fragment{\times \{L, R, S\}^k} \]
\[ \fragment{ \delta(q, a_1, \ldots, a_k) = (q', b_1, \ldots, b_k, m_1, \ldots, m_k) } \]
- Theorem: For every multitape Turing machine \(M\) there exists a single-tape Turing machine \(S\) such that \(L(M) = L(S)\). Furthermore if \(M\) is total, then \(S\) is total.
- Proof idea: Construct \(S\) to simulate \(M\) on a given input.
Simulating a Multitape Turing Machine

In order to define \(S\), we have to describe how it:
- Encodes any configuration \(C_M\) of \(M\) as a configuration \(C_S\) of \(S\).
- Initially sets up its tape to simulate \(M\) (i.e., gets to the configuration encoding \(M\)’s initial configuration).
- Moves from \(C_S\) to a new configuration representing \(C'_M\) when \(C_M \to C'_M\).
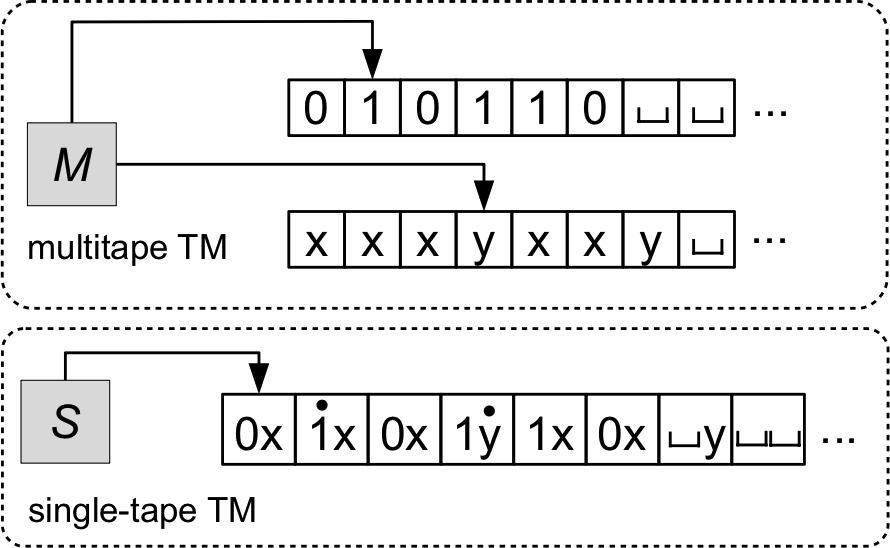
Simulating Multiple Tapes: Configuration Encoding
- A configuration of \(C_M\) looks like: \[ C_M = (q, p_1, \ldots, p_k, w_1, \ldots, w_k) \]
- We need to encode \(k\) tape head positions and \(k\) tape contents!
- Idea: encode that a head is pointing at a character on the tape with a special marker.
- Graphically: replace \(a \in \Gamma\) with \(\markedCharacter{a}\) (e.g., \(\markedCharacter{\string{x}}, \markedCharacter{\string{0}}, \markedCharacter{\#}\)).
- Formally: we can represent marked/unmarked characters as tuples in \(\Gamma \cross \{\circ, \bullet\}\) (e.g., \((\string{x}, \circ)\) and \((\string{x}, \bullet)\)).
- To encode tape contents \(w_1\), \(w_2\), \(\ldots\), \(w_k\), we have a few options:
- Sipser’s approach: concatenate the tape contents with \(\#\) delimiters
marking their starts and ends (assuming \(\# \notin \Gamma\)). \[ \# w_1 \# w_2 \# \cdots \# w_k \# \] - Our approach: form “compound symbols” to represent the characters at the same cell of each tape.
- Graphically: a single smushed-together symbol like \(\string{b} \markedCharacter{\string{0}} \string{x}\) to represent three tapes with respective symbols \(\string{b}, \string{0}, \string{x}\).
- Formally: an element of \((\Gamma \cross \{\circ, \bullet\})^k\)
- Sipser’s approach: concatenate the tape contents with \(\#\) delimiters

Simulating Multiple Tapes: Setup and Execution

- Given input \(x\), setup is easy in both variants.
- Sipser: \(\# \markedCharacter{x_1} x_2 \cdots x_n \# \markedCharacter{⎵} \# \cdots \# \markedCharacter{⎵} \#\).
- Write \(\# \markedCharacter{x_1}\).
- Copy the rest of the input from \(x\) with no markers.
- Write \(k - 1\) copies of \(\# \markedCharacter{⎵}\), followed by a final \(\#\).
- Ours: \(\markedCharacter{x_1}\markedCharacter{⎵}^{k - 1}\; x_2{⎵}^{k - 1} \; \cdots \; x_n{⎵}^{k - 1}\)
- Write \(\markedCharacter{x_1}\markedCharacter{⎵}^{k - 1}\)
- For each remaining character, write \(x_1⎵^{k - 1}\)
- Sipser: \(\# \markedCharacter{x_1} x_2 \cdots x_n \# \markedCharacter{⎵} \# \cdots \# \markedCharacter{⎵} \#\).
- To simulate each transition:
- Scan through the tape until all \(k\) markers are found, and remember the symbols under them.
This is a finite amount of information: \((a_1, \cdots, a_k) \in \Gamma^k\)) - \(M\)’s transition function can now be consulted \(\delta(q, a_1, \cdots, a_k)\).
- Do another pass through the tape the beginning, writing the appropriate symbols around each marked character to update the character and move the marker.
- Scan through the tape until all \(k\) markers are found, and remember the symbols under them.
“Weaker” Variants
- We can also impose more limitations on Turing machines without reducing their computational power:
- Move-right-or-reset: the tape head can only move right or reset to the leftmost position.
- Use two stacks instead of a tape.
(But using just one stack reduces the power to a DPDA, incapable of deciding even certain CFLs - One queue
- Three counters: three integers that we can increment, decrement, and check if they hit zero
(But using one counter is equivalent to a unary single-stack machine,
which can decide \(\setbuild{0^n 1^n}{n \in \mathbb{N}}\) but not \(\setbuild{w = \reverse{w}}{w \in \binary^*}\))
Algorithms
- Informally, an algorithm is a sequence of steps that can be followed to solve a problem.
- Formally, we can define an algorithm as a procedure that can be implemented by a Turing machine.
- However, after gaining some practice with Turing machines, we typically won’t specify the details of the machine.
- Instead we can describe algorithms formally and precisely with a higher-level language (like Python).
- We will argue that implementing a Python program on a Turing machine, while slower, won’t change its “complexity class.”
(See HW3)
Turing Machines vs. Programs
Consider the problem of comparing two strings \(x\) and \(y\) to see if they are equal.
This is trivial to do in code:
def compare(x, y): if len(x) != len(y): return False for i in range(len(x)): if x[i] != y[i]: return False return Trueand it’s easy to count the number of “operations” run.
How can we do this with a Turing machine?
- Decision problem: check if \(x \# y\) is in the language \(L = \setbuild{w \# w}{w \in \Sigma^*}\).
- The Turing machine would need to:
- Zig-zag across the tape to corresponding cells on each side of the \(\#\).
- If the symbols mismatch, reject.
- If they match, cross them off by writing \(\string{x}\) symbols.
- When all symbols to the left of \(\#\) are crossed off, accept if remaining symbols are all \(\#\) or \(\string{x}\); reject otherwise.
- Zig-zag across the tape to corresponding cells on each side of the \(\#\).

Object Encoding for Turing Machines
- But programs can obviously operate on fancier objects than strings.
How can a Turing machine do this too? - For example, how can a TM read a graph?
Node and edge lists: \(\encoding{G} = \fragment{(1,2,3,4)}\fragment{((1,2),(2,3),(3,1),(1,4))}\)
We use \(\encoding{O}\) to denote the encoding of an object \(O\) as a string in \(\binary^*\). We can encode multiple objects with \(\encoding{(O_1, O_2, \ldots, O_k)}\) or just \(\encoding{O_1, O_2, \ldots, O_k}\).
Adjacency matrix: \[ \fragment{\begin{bmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{bmatrix}} \fragment{\quad \Longrightarrow \quad \encoding{G} = } \fragment{0111101011001000} \hspace{15em} \]
How can we determine the number of nodes?
(labels don’t matter).
Object Encoding for Turing Machines
- But programs can obviously operate on fancier objects than strings.
How can a Turing machine do this too? - For example, how can a TM read a graph?
- The choice of encoding \(\encoding{\cdot}\) can matter a lot for practical reasons
- What is the size of the adjacency matrix representation for a graph with \(n\) nodes? \(n^2\)
- What about the node+edge list representation for a graph with \(n\) nodes and \(m\) edges?
Proportional to \(n + m\). For sparse graphs \(m \ll n^2\)… - This sort of difference is a big deal, e.g., in high-performance computing.
- But for theoretical analysis we will show any “reasonable” encoding is good enough (won’t change whether an algorithm is polynomial time or not).
