Title

ECS 120 Theory of Computation
NP-Completeness and Reductions, Pt 2
Julian Panetta
University of California, Davis

Recall: definition of Polynomial-Time Reducibility

A function \(f: \binary^* \to \binary^*\) is polynomial-time computable if there exists a polynomial-time algorithm that, given input \(x\), computes \(f(x)\).

Let \(A, B \subseteq \binary^*\) be decision problems. We say \(A\) is polynomial-time reducible to \(B\)
if there is a polynomial-time computable function \(f\) such that for all \(x \in \binary^*\):

\[ \fragment{x \in A \iff f(x) \in B} \]

We denote this by \(A \le^P B\).

\(A \le^P B\) means: “B is at least as hard as A” (to within a polynomial-time factor).

Which of the following are possible lengths of \(f(x)\)?

  • \(|x|\)
  • \(\log{|x|}\)
  • \(2^{|x|}\)

\(|f(x)| \le |x|^c\) if \(f\) is computable in time \(n^c\) for some constant \(c\).

Visual Schematic of Polynomial-Time Reduction

\[ A \le^P B \]

“Reducing from \(A\) to \(B\)”

\[ x \in A \iff f(x) \in B \]

  • Needn’t be \(1\)-\(1\) or onto!
  • Just needs to map:
    • \(x \in A\) to \(f(x) \in B\).
    • \(y \notin A\) to \(f(y) \notin B\).

Recall: Example Reduction to Bound Complexity of \(\probClique\)

from itertools import combinations as subsets
def reduction_from_independent_set_to_clique(G, k):
    V, E = G
    Ec = [ {u,v} for (u,v) in subsets(V,2)
            if {u,v} not in E and u!=v ]
    Gc = (V, Ec)
    return (Gc, k)

# Hypothetical polynomial-time algorithm for Independent Set
def independent_set(G, k):
    Gp, kp = reduction_from_independent_set_to_clique(G, k)
    return clique_algorithm(Gp, kp)

# Hypothetical polynomial-time algorithm for Clique
def clique_algorithm(G, k):
    raise NotImplementedError("Not implemented yet...")
data/images/complexity/ind_set_clique_complete.svg
  • We conclude that \(\probIndSet \le^P \probClique\).
  • \(\probClique\) is at least as hard as \(\probIndSet\).
  • Since reduction_from_independent_set_to_clique also happens to work in the other direction
    (just complement again!), we can conclude also: \(\probClique \le^P \probIndSet\).

Implications of \(A \le^P B\)

Let’s now formalize what we mean by “\(B\) is at least as hard as \(A\)”

Theorem: If \(A \le^P B\) and \(B \in \P\), then \(A \in \P\).

Proof:

  • Since \(B \in \P\), there exists an algorithm \(M_B\) for \(B\) that runs in time \(n^k\) for some constant \(k\)

  • Since \(A \le^P B\), there exists a polynomial-time reduction \(f\) from \(A\) to \(B\)
    (running in time \(n^c\) for some constant \(c\)).

  • We can construct an algorithm \(M_A\) deciding \(A\) simply by composing \(f\) and \(M_B\): \[ M_A(x) = M_B(f(x)) \]

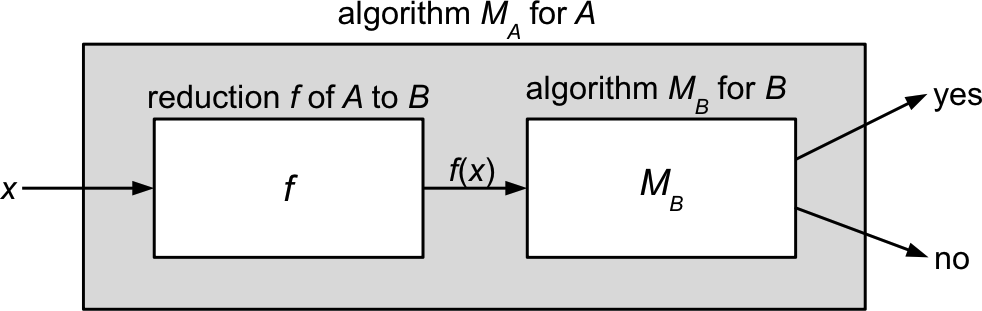
    data/images/complexity/reduction_schematic.png

  • What is the time complexity of \(M_A\)? Let \(n = |x|\).

    • \(O(n^c)\) for \(f(x)\), plus \(O(m^k)\) for \(M_B(f(x))\), where \(m = |f(x)|\).
    • Since \(m = O(|x|^c)\), the full time complexity is: \[ O(n^c) + O(O(|x|^c)^k) \fragment{= O(n^c + n^{ck})} \fragment{= O(n^{ck})} \fragment{\quad \implies \quad A \in \P} \]

Implications of \(A \le^P B\)

Let’s now formalize what we mean by “\(B\) is at least as hard as \(A\)”

Theorem: If \(A \le^P B\) and \(B \in \P\), then \(A \in \P\).

  • If the fastest algorithm for \(B\) runs in time \(t(n)\), then the fastest algorithm for \(A\) takes no more than \(p(n) + t(p(n))\) where \(p(n)\) is the polynomial running time of \(f\).
  • These runtimes are both “polynomially equivalent.”

Corollary: If \(A \le^P B\) and \(A \notin \P\), then \(B \notin \P\).

This corollary is the way we typically use reductions:
we know/believe \(A\) is hard, and want to show \(B\) is at least as hard.

Which Direction to Reduce

Suppose we want to show that \(\probSAT\) is at least as hard as \(\probHamPath\).

Which problem should we reduce to which?

  • Reduce from \(\probSAT\) to \(\probHamPath\)
  • Reduce from \(\probHamPath\) to \(\probSAT\)

\[ \probHamPath \le^P \probSAT \]

\[ \probHamPath \overset{f}{\longrightarrow} \probSAT \]

  • We equivalently want to show \(\probHamPath\) is “at least as easy” as \(\probSAT\).
  • We do this by exhibiting an algorithm for \(\probHamPath\):
    • Reduce to \(\probSAT\) via \(f\).
    • Run the algorithm for \(\probSAT\).

Reductions Between Problems of Different Types

  • The reduction from \(\probClique\) to \(\probIndSet\) (and vice versa) was not too surprising since the concepts of cliques and independent sets are closely related.
  • But reductions can remarkably creative, drawing connections between seemingly unrelated problems.
  • To see this, let’s consider another problem known to be as hard as \(\probSAT\), called \(\probThreeSAT\).
  • \(\probThreeSAT\) is a special case of \(\probSAT\) where the Boolean formula is in a special form.

Reductions Between Problems of Different Types: \(\probThreeSAT\)

A Boolean formula is in conjunctive normal form (CNF) if it is a conjunction of clauses,
where each clause is a disjunction of literals. Example:

\[ \phi = \underbrace{(x \lor \overline{y} \lor \overline{z} \lor w)}_\text{Clause 1} \land \underbrace{(z \lor \overline{w} \lor x)}_\text{Clause 1} \land \underbrace{(y \lor \overline{x})}_\text{Clause 3} \]

\(\encoding{\phi} \in \probSAT\) iff we can pick one literal from each clause to set to “1” without conflicts!

A literal is a variable \(x\) or its negation \(\overline{x} = \neg x\).

A Boolean CNF formula \(\phi\) is a 3-CNF formula if each of its clauses has exactly 3 literals.
Example: \[ \fragment{\phi = (x \lor \overline{y} \lor \overline{z}) \land (z \lor \overline{y} \lor x)} \]

\[ \probThreeSAT = \setbuild{\encoding{\phi}}{\phi \text{ is a satisfiable 3-CNF formula}} \]

This turns out to be just as hard as \(\probSAT\)!

Reductions Between Problems of Different Types: \(\probThreeSAT\)

\[ \probThreeSAT = \setbuild{\encoding{\phi}}{\phi \text{ is a satisfiable 3-CNF formula}} \]

\[ \probIndSet = \setbuild{\encoding{G, k}}{ G \text{ is an undirected graph with a } k\text{-independent set}} \]

  • We’ll now show that \(\probIndSet\) is at least as hard as \(\probThreeSAT\). \[ \probThreeSAT \le^P \probIndSet \]
  • This is not obvious how to do: \(\probIndSet\) involves graphs and \(\probThreeSAT\) involves formulas.
  • Our reduction will need to convert clauses of a 3-CNF formula into graph structures.
  • These structures built by the reduction are called gadgets
    • The literals of the formula will be “simulated” by nodes in the graph.
    • The clauses will be “simulated” by triplets of nodes.

Reductions Between Problems of Different Types: \(\probThreeSAT\)

\[ \probThreeSAT = \setbuild{\encoding{\phi}}{\phi \text{ is a satisfiable 3-CNF formula}} \]

\[ \probIndSet = \setbuild{\encoding{G, k}}{ G \text{ is an undirected graph with a } k\text{-independent set}} \]

Theorem: \(\probThreeSAT \le^P \probIndSet\).

Proof:

  • Given a 3-CNF formula \(\phi\), our reduction must produce a pair \((G, k)\) such that: \[ \encoding{\phi} \in \probThreeSAT \; \iff \; \encoding{G, k} \in \probIndSet \]

  • Set \(k\) equal to the number of clauses in \(\phi\).

  • To simplify notation, we write \(\phi\) as: \[ \phi = (a_1 \lor b_1 \lor c_1) \land \fragment{(a_2 \lor b_2 \lor c_2) \land} \fragment{\ldots \land (a_k \lor b_k \lor c_k)} \] where \(a_i, b_i, c_i\) are the three literals in clause \(i\).

G will have \(3k\) nodes,
one for each literal in \(\phi\).

Example Gadget Construction

\[ \phi = (x \lor x \lor y) \land (\overline{x} \lor \overline{y} \lor \overline{y}) \land (\overline{x} \lor y \lor y) \hspace{6em} \]

Is this formula satisfiable?
Yes: \(x = 0, y = 1\).

\(\encoding{\phi} \in \probThreeSAT\) iff we can pick
one literal from each clause
to set to “1” without conflicts!

Reductions Between Problems of Different Types: \(\probThreeSAT\)

Theorem: \(\probThreeSAT \le^P \probIndSet\).

Proof:

  • Given a 3-CNF formula \(\phi\): \[ \phi = (a_1 \lor b_1 \lor c_1) \land (a_2 \lor b_2 \lor c_2) \land \ldots \land (a_k \lor b_k \lor c_k) \] we produce a pair \((G, k)\) such that: \[ \encoding{\phi} \in \probThreeSAT \; \iff \; \encoding{G, k} \in \probIndSet \]

  • Set \(k\) equal to the number of clauses in \(\phi\).

  • Create one node in \(G\) for each literal in \(\phi\).
  • Create edge {u, v} in \(G\) if and only if:
    • \(u\) and \(v\) correspond to literals in the same clause (triple), or
    • \(u\) is labeled \(x\) and \(v\) is labeled \(\overline{x}\) for some variable \(x\) (or vice versa).

We can generate these edges in polynomial time by looping over all pairs of nodes (\(O(|V|^2)\))
and checking the these two conditions by scanning through \(\phi\). (Python code in lecture notes)

Reductions Between Problems of Different Types: \(\probThreeSAT\)

Proof that \(\encoding{\phi} \in \probThreeSAT \; \iff \; \encoding{G, k} \in \probIndSet\):

  • Direction 1: \(\phi\) satisfiable \(\implies\) \(G\) has a \(k\)-independent set.
    • Suppose \(\phi(w) = 1\) (\(w\) is a satisfying assignment).
    • Then \(w\) makes at least one literal in each clause true.
    • Construct \(k\)-independent set \(S\) by arbitrarily selecting one node from each clause labeled by a true literal.
    • For every \(u, v \in S\) both conditions used to create edges are false.
    • So \(u\) and \(v\) are not connected by an edge, and \(S\) is a valid \(k\)-independent set in \(G\)!
  • Direction 2: \(G\) has a \(k\)-independent set \(\implies\) \(\phi\) satisfiable
    • Given an \(k\)-independent set \(S\), we construct assignment \(w\) by marking variables corresponding to non-complemented literals in \(S\) as true.
    • Every node in \(S\) must correspond to a different clause due to condition \(1\).
    • Since there are \(k\) clauses and \(|S| = k\), each clause must have at least one true literal marked.
    • The edges in \(G\) between nodes for “conflicting” literals mean \(w\) does not set \(x\) and \(\overline{x}\) to true at the same time for any \(x\). Hence \(w\) is a valid satisfying assignment!