ECS110 Lecture Notes for Monday, October 23'rd 1995
Professor Rogaway conducting
Lecture 11
Scribe of the day: These things include the name, number of arguments and types of arguments of the function
Lectures 7-8
12) Strings
13) Knuth-Morris-Pratt (KMP) function for matching substrings
Lectures 9-10
14) The stack as an ADT
15) Use of stacks
16) Matching "(" , ")" , ...
17) Maze exploration: explicit bookkeeping
18) Expression evaluation
A) Infix, prefix, postfix notation
B) Infix -> postfix
C) Evaluation in postfix
D) Tree representation of an expression
Queues
Data of a Queue
Queues (of type T)
Data: an ordered sequence of elements from T:
n,(X1, ... , Xn) where X1, ... , Xn is an element of T
void enqueue (T x) //Replace (X1, ... , Xn) with (X1, ... Xn ... X); increment n;
T dequeue() //If empty: replace (X1, ... , Xn) with (X2...Xn), decrement n and return x;
Int empty() {return front == rear;};
This (an array) is a poor representation of a queue because the queue can fill up quickly!
Circular Queues
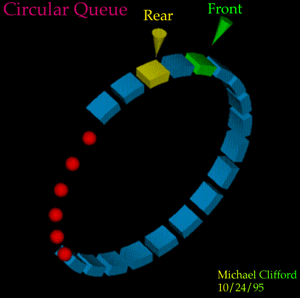
The queue is full when rear + 1 mod (queuesize) == front
In this illustration, the circular queue is full, because rear + 1 mod (queuesize) == front
B
Int full() {return (rear+1) % MAX == front;}
void enqueue (T element){
if (full()) error();
A[rear] = element;
rear = (rear+1) % MAX;
};
T dequeue(){
if empty() error();
else{
int tmp = front;
front = (front + 1) % MAX;
return A[tmp];
}
}
Queues

- Data: an ordered sequence of elements from T:
n,(X1, ... , Xn) where X1, ... , Xn is an element of T

-
if (full()) error();
A[rear] = element;
rear = (rear+1) % MAX;
};
- if empty() error();
else{
int tmp = front;
front = (front + 1) % MAX;
return A[tmp];
}