ECS110 Lecture Notes for Friday, November 3rd 1995
Professor Rogaway conducting
Lecture 15
Scribe of the day:
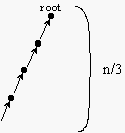
How long will n operation drawn from makeset, union, and find take?
makesets n/3 \
union n/3 |=> (n^2)/9 = Theta(n^2)
find n/3 /
 Improving the Efficiency
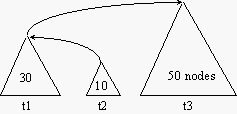
1. Union by size
Improving the Efficiency
1. Union by size
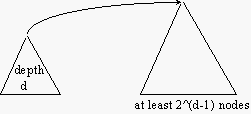
 lemma: In a sequence of makeset, union, and find operations,
if the depth of some tree is d then that tree has at least
2^(d-1) nodes (using union by size)
proof: By induction.
basis : if d = 1 : 2^(d-1) = 1
if d > 1 : Assume lemma holds on depth <= d :
prove holds d+1
lemma: In a sequence of makeset, union, and find operations,
if the depth of some tree is d then that tree has at least
2^(d-1) nodes (using union by size)
proof: By induction.
basis : if d = 1 : 2^(d-1) = 1
if d > 1 : Assume lemma holds on depth <= d :
prove holds d+1
 Therefore, the tree of depth d+1 has >= 2^d nodes.
O(n^2) -------> O(n lg n)
2. Collapsing finds
Therefore, the tree of depth d+1 has >= 2^d nodes.
O(n^2) -------> O(n lg n)
2. Collapsing finds
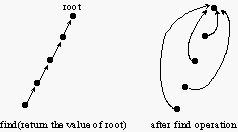
lemma : Using collapsing finds n operations takes O(n lg n)
Th : Using Union by size and collapsing finds, a sequence of n operations
on our data structure (makeset, union, finds) takes O(n lg* n)
lg* n is the least k such that :
lg lg lg . . . . . . . . lg n <= 1
`--------------------------'
k
lg* (2) = 1
lg* (4) = 2
lg* (16) =3
lg* (65536) = 4
lg* (2^65526) = 5




