Today:
  Dijkstra's Algorithm
  Fibonacci Heaps

Reading:
  9.4,9.5



Dijkstra's Algorithm

Goal: To find the shortest path to each node

length(v,w)>=0
set the upper bound on each node equal to infinity


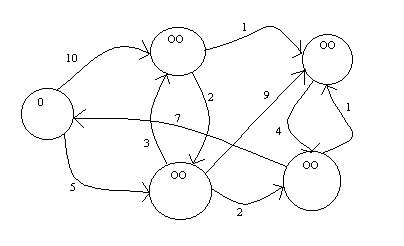shortest path to s is s = 0
in order of cheapest nodes



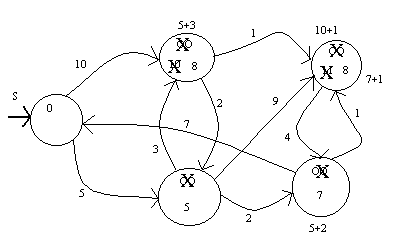look at outgoing arc and decide is it connects to a node


Pseudo Code:

  Let S <- {s}
  d[s] <- 0; d[v] <- oo  (for all v in V not equal to s)
  while S != v
    - find a v with minimum d[v]
    - S <- S union {v}
    - for all w <- adj(v) - S
	if d[v] + length(v,w) < d[w]
   	d[w] <- d[v] + length(v,w)


another example

length(v,w)>=0


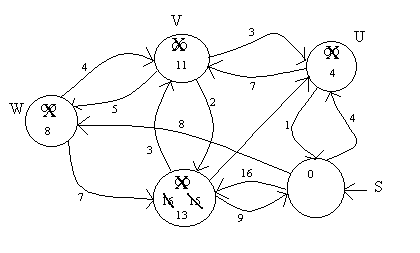0 label is fixed, put in set. Then check all outgoing vertices

record predecessor
  (13,v) tells where 13 came from 
  (11,u)
  (4,s)
  
  can recover a path, finds the shortest path to 13
  (s,u,v,y)



Using a heap to implement Dijkstra's algorithm

Heap h;

   for i <- 1 to n do
    { node[i].d = infinity; }
      node[s].d = 0;
   for i <- 1 to n do
    { h.insert(node[i]); }
   for i <- 1 to n do  {
     v = h.delete_min();
     for eack w in adj(v)
       if v.d + length(v,w) < w.d
	delta = w.d-v.d-length(v,w)
        h.decrease_key(w,delta) 
    }


efficiency of Algorithm

  n calls to insert
  n calls to delete_min
  m calls to decrease_key
    (m = # edges, at least the size of n)

try to find a more efficient method



heap implementations:

              | Sorted        | (min)         | Fibonacci
              | Linked List   | binary heap   | Heap
------------------------------------------------------------              
              |               |               | 
insert        | theta(n)      | theta(lgn)    | theta(1) 
amortized             
------------------------------------------------------------              
              |               |               | 
delete_min    | theta(1)      | theta(lgn)    | theta(lgn) amortized
------------------------------------------------------------            
              |               |               |
decrease_key  | theta(n)      | theta(lgn)    | theta(1) amortized
------------------------------------------------------------
              |               |               |
Total Time    | O(n^2+n+mn)   | O(nlgn+mlgn)  | O(n+nlgn+m)
              | O(mn)         | O(mlgn)       | O(m+nlgn)



binomial heaps

    - a doubly linked list of heap ordered binomial trees
    - each node records
        1. degree
        2. youngest child
        3. net older sibling
    - one pointer, min, to the tree with the smallest root