ECS 110 Lecture Notes for Wednesday, November 29, 1995

ECS110 Lecture Notes for Wednesday, November 29, 1995

Professor Rogaway conducting

Lecture 24
Scribe of the day: Kenneth C. Lee (Cyber Ferrari)

Today

Binomial Trees

// max degree of its node appears at root
depth of a B_t = t

Combination 1:

Combination 2:

Combine Fig. 2 and 3, then you will get Fig. 4.

Now, go back to Fig. 2. We want to do a delete-min on it.
This requires not just deleting the minimum node, but also
recombining the current trees to maintain the binomial tree
properties for the data structure

Step 1:

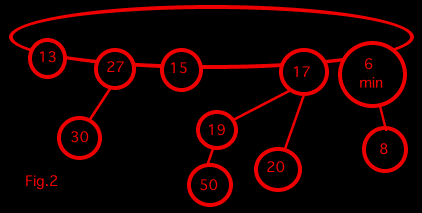
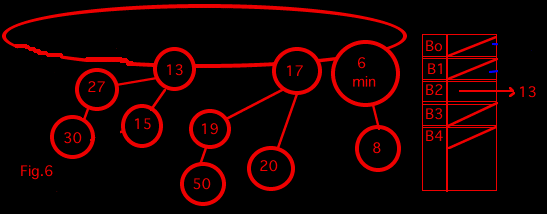
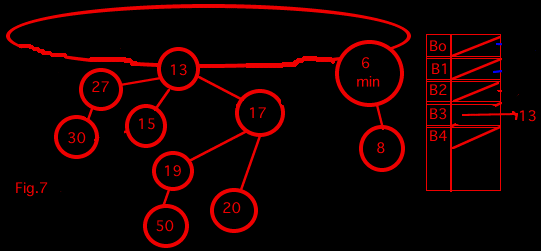
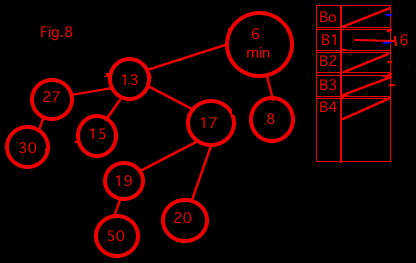
The table on the right in the diagram is a table pointing to binomial trees of different degrees. When we look at a tree, we determine the degree and point to it from the table. If the table is already pointing to a tree of that degree, we combine the two together to make a tree with one degree higher. This means that when we look at the tree containing 15, we already have a tree of degree 0 and so we combine those two trees to get a tree of degree 1.

Step 2:

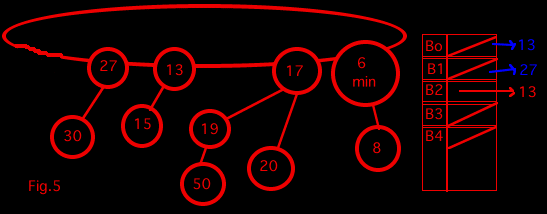
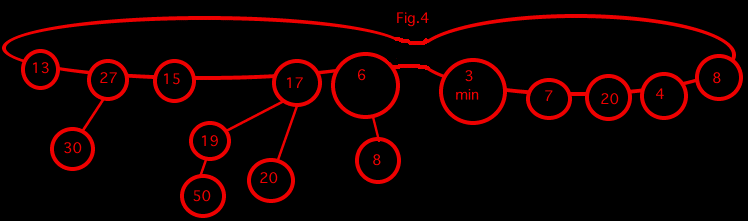
We keep looking at the trees and recombining them from the table until we can do this no more.

Step 3:

Step 4:

Now, the tree is done

Potential Functions:

Pfcn maps Data Structure -> Positive Number

₀

Cost of a sequence of t operations(Op₁, . . . ,Op_t) = cost1 + ... + costt

Actual Cost = Cost of Op₁ + change of Pfcn1 + . . .

+ Cost of Op_t + change of Pfcnt

- ( change of Pfcn₁ + . . . + change of Pfcn_t )

Actual Cost = AmCost of Op₁ + . . .

+ AmCost of Op_t

- ( Pfcn₁ - Pfcn₀ + Pfcn₂ - Pfcn₁ + . . . + Pfcn_t - Pfcn_t-1 )

Actual Cost = AmCost - Pfcn_t

Therefore Actual Cost <= AmCost

Note: delta$ is the same as the change in Pfcn (Pfcn and $ are the same thing)

Potential(Pfcn) of the Data Structure = Number of Trees (roots) in it.

t = number of Trees in the data structure.

c = number of tree get combined in deletemin operation.

NUMber of trees after combining = t - c <= Degree of element to delete O(log n).