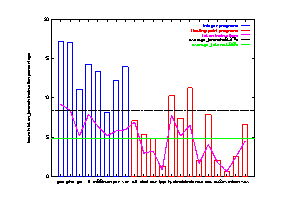
Figure 12 The Frequencies of Conditional Branches
To evaluate the performance of the seven different schemes, we first studied the branch behavior of the 21 benchmark programs that we use for this project. From this information, we are able to calculate the accuracy limit on the performance of a static predictor. Second, we give a comprehensive comparison of the seven schemes. Third we look at the effect of varying the buffer size on prediction accuracy for some dynamic schemes. Fourth, the effect of context switching on branch prediction is discussed. Finally, we look at an interesting benchmark program from SPECint95-beta.
| Program | Traced_Inst# | Dynamic_Branch# | Taken_Branch# | Taken_Branch% |
| gcc | 6186539354 | 1057556947 | 566093312 | 53.53 |
| ghost | 4057743776 | 690986805 | 339710533 | 49.16 |
| go | 9800796393 | 1078696639 | 504611777 | 46.78 |
| li+ | 7007645073 | 1000000000 | 551847194 | 55.18 |
| m88ksim+ | 7507989139 | 1000000000 | 479341651 | 47.93 |
| numi+ | 12355029197 | 1000000000 | 639221685 | 63.92 |
| perl+ | 8234202623 | 1000000000 | 474993437 | 47.50 |
| vortex+ | 7195515374 | 1000000000 | 425973672 | 42.60 |
Table 4. Branch behavior of benchmark programs from SPEC95int-beta
| Program | Traced_Inst# | Dynamic_Branch# | Taken_Branch# | Taken_Branch% |
| alivinn | 6792027933 | 480143481 | 469154917 | 97.71 |
| doduc | 1644410091 | 87092576 | 48388199 | 55.56 |
| ear | 14506557248 | 705032704 | 466983346 | 66.24 |
| fpppp | 8463667939 | 106307360 | 67686215 | 63.67 |
| hydro2d | 6627612755 | 680214394 | 515386882 | 75.77 |
| mdljdp2 | 4206065214 | 309377515 | 215543933 | 69.67 |
| mdljsp2 | 3011635408 | 338499291 | 195972810 | 57.89 |
| nasa7 | 11104431137 | 217326271 | 186014771 | 85.59 |
| ora | 2029511987 | 158386472 | 82174861 | 51.88 |
| su2cor | 8055850151 | 165611544 | 140751098 | 84.99 |
| swm256 | 9862718926 | 66039940 | 61056566 | 92.45 |
| tomcatv | 1261279753 | 31605162 | 30958962 | 97.96 |
| wave5 | 4331716191 | 286632343 | 194798779 | 67.96 |
Table 5. Branch behavior of benchmark programs from SPEC92fp
Conditional branch frequencies dramatically affect machine pipeline performance. Therefore, it is important to look at the percentage of conditional branches. Figure 12 lists the conditional branch frequencies for the 21 benchmark programs used in this study. The x-axis lists the 21 benchmark programs starting with the 8 integer programs. The y-axis shows the percentage of conditional branches. The integer programs show conditional branch frequencies of 8% to 17%, with numi having the lowest. As mentioned in the previous section, among all integer programs, numi is the only one written in Fortran and has the highest FP instruction percentage -- 10.2%. All the other integer programs are written in C. The FP programs have lower percentage of conditional branches then integer programs. They show frequencies between 1% to 11%. The average frequency for the 8 integer programs is about 14% and 5% for the 13 FP programs.

Figure 12 The Frequencies of Conditional Branches
In Figure 13, the frequencies of taken conditional branches are given. As in Figure 12, the x-axis lists the 21 benchmark programs, and the y-axis gives the percentage of taken conditional branches. The first 8 programs are integer programs. The horizontal dash line represents the average frequency for all the 21 programs. All of the 8 integer programs are below this average. numi is close to the average for the same reason in the earlier paragraph. Notice some of the FP programs have almost 100% taken frequency, such as alvinn and tomcatv. The average for the integer programs is about 50% and 75% for the FP programs. As you will see later, this frequency is directly related to prediction performance of all the predictors. Generally speaking, the higher the taken frequency, the higher the prediction accuracy. This is also shown in the earlier discussion of tracing instruction number. The prediction accuracy curves in Figure 10 have a similar shape as the branch taken percentage curve in Figure 11. FP programs are easier to predict than integer programs with low frequency of taken branches.
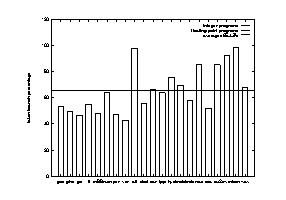
Figure 13 Percentage of conditional branches that are taken
The bias of a branch describes how strongly this branch tends to be taken or to be not taken. Profiling based Static predictors work well because that most of the dynamic branches executed are strongly biased. Figure 14 shows the bias over all integer benchmarks, over all FP benchmarks, and over all the 21 benchmarks. The average of each group is used. The x-axis shows for a particular branch the percentage of executed branches that are taken. Branches within 5% are grouped together as one group. The y-axis shows the percentage of branches that have a certain bias. The less frequent the number of branches in the middle, the better the performance of the perfect static predictor. We notice that the FP programs are more biased than the integer programs.
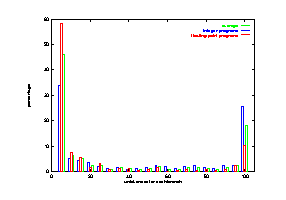
Figure 14 Branch bias, weighted by execution frequency.
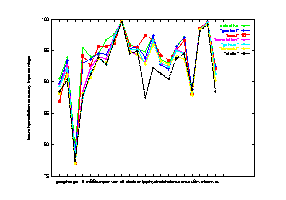 |
|---|
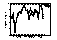
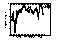
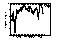
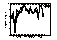
 |
| Figure 15 Seven schemes performance on the 21 benchmark programs |
| (Click the following hyper texts to have detailed views of the comparison.) |
| comparison of static, bimodal and common-correlation schemes |
| comparison of gshare, common-correlation, local and gselect schemes |
| comparison of gselect, local and selective schemes |
| comparison of gselect, local and common-correlation schemes |
| comparison of static, bimodal and selective schemes |
Figure 16 Seven schemes average prediction accuracy over the
21 benchmark programs
| Benchmarks | Schemes ordered by performance (from worst to best) | ||||||
|---|---|---|---|---|---|---|---|
| INT | static | bimodal | gshare | correlation | local | gselect | selective |
| 89.8% | 89.8% | 90.3% | 90.8% | 91.3% | 91.8% | 92.7% | |
| FP | static | bimodal | correlation | gshare | gselect | selective | local |
| 93.3% | 94.4% | 94.7% | 94.7% | 95.3% | 95.5% | 95.6% | |
| ALL | static | bimodal | gshare | correlation | local | gselect | selective |
| 92.0% | 92.6% | 93.0% | 93.2% | 93.9% | 93.9% | 94.4% | |
Table 6. Performance summary of the seven schemes
We observe the following:
The results are shown in Figure 17, with curves for the three dynamic schemes. The curve for the bimodal scheme goes flat when the number of 2-bit counters gets above about 5000. This agrees with results from previous research. Therefore, for the bimodal scheme, buffer size is not a limiting factor when it is more than 8K bits (4K 2-bit counters). The bimodal scheme behaves this way because in a typical run of program, 5000 different branches is considered to be large. Shown in Table 1 and Table 2, excluding gcc and vortex, all benchmarks studied have only between 1000 and 5000 static conditional branches. The common correlation scheme still has noticeable improvement with increased buffer size till 20K bits or 10K 2-bit counters. Even when the buffer size reaches 200K bits, the gselect scheme still shows significant improvement if the correlation depth is also increased accordingly.
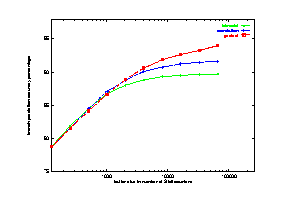
Figure 17 Effects of varying branch prediction buffer size
The results are shown in Figure 18, with curves for bimodal, correlation, and gselect. The three horizontal lines in the figure show the prediction accuracies for each scheme in the case of no context switch. For all three schemes, we observe that the effect of context switches on prediction rate decreases as the number of instructions between context switches gets larger. We see very little effect after the number of instructions is over 1 million.
Since the increased speed in CPUs, the number of instructions between context switches is getting larger. For a 50-MIPs machine, it is about 3 million instructions assuming the commonly used 16 context switches per second on a UNIX system. Therefore, context switching has little effect on branch prediction accuracy. However, threads and multiprocessing are increasing in importance. The number of instructions between context switches for these lightweight processes sometimes is much shorter than conventional context switches. For this reason, the effect of context switches should not be overlooked.
We also notice that for less complicated schemes such as bimodal, the effect of context switches is not as evident as for some more complicated schemes such as gselect. This indicates that complicated schemes need longer time to warm up than simple schemes.
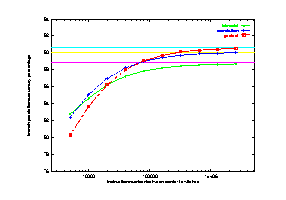
Figure 18 Effects of context switching on prediction accuracy
go is a special version of the "Go" program, "The Many Faces of Go", developed for use as a part of the SPEC benchmark suite. As described in the description file with the benchmark, go is an artificial intelligent game program. It is a computation bound integer benchmark and uses a very small amount of FP only during initialization to set up an array of scaled integers. It uses almost no divides, and few multiplies. Most data is stored in single dimensioned arrays specifically to avoid multiplies. This program has been extensively optimized using gprof to tune for maximum performance. Some inner loops have been unrolled in C. It features many small loops and lots of control flow -- if-then-else. This feature of go causes all the branch prediction schemes which take advantage of long looping structures to perform poorly. Does this say that complicated compiler optimization will change the program branch behavior and the prediction accuracy?
Figure 19 shows the bias of go with comparison to gcc and the average for the 8 integer programs. The curves for both gcc and the integer average show clear U-shape. However, the curve for go is quite flat. There are about same number of branches for each 5% interval of un-takenness. This distribution of branches causes various predictors to perform poorly. This result also indicates that the branch behavior is the most important parameter in determining the prediction accuracy of each scheme.
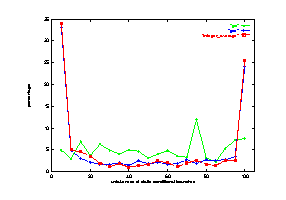
Figure 19 Profiling information for go
We look at the effect of increasing buffer size on prediction accuracy using go as the testing benchmark. For this part of the study, we used the gselect scheme. We varied the branch prediction buffer from 256 bytes to 64K bytes. For each buffer size, the history depth also need to be varied. Without increasing the correlation depth, increasing buffer size does not gain much improvement.
Figure 20 shows the results from this study. The x-axis shows the number of global history bits used (history depth). The y-axis shows the prediction accuracies. There is a curve associated with each buffer size. For each buffer size, there is one with the best prediction rate. We use another curve to connect all these points. For the 256 bytes buffer, the best prediction accuracy is about 76%. If 64K bytes buffer is in use, the best prediction accuracy can go up to about 88%, which has a 50% improvement in miss predict rate.
From the figure, we notice that for go, a highly correlated program, increasing the number of global history bits can help to improve the prediction accuracy. Since there are lots of if-then-else control structures in the benchmark, the direction of a branch usually depends on the outcome of others. Therefore, the predictor needs high correlation depth, which is larger than 15 indicated by the 64KB curve.
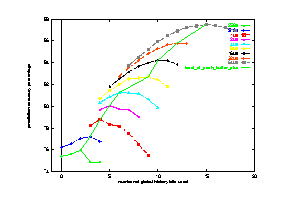
Figure 20 Effects of increasing branch prediction buffer size on go using gselect