Although most games elude full-scale analysis, many can be simplified
and analyzed.
For example, poker is most excitingif there are 4 to 5 players - at
least.
But straight poker with a pot limit and two-players can be analyzed
in a theretical framework. For this case, the optimal strategy for the
opening player
says that he should ALWAYS bet on the first round with J9632 or worse
but checking (and folding if bet into) with hands in the range J9632-22J109.
That is one should always bluff with a bad enough hand but never with a
slightly better one.
The question we are more interested is this: What should each player
do, if all th eplayers were doing the best for themselves as they possibly
could?
There are many forms of Nim. We shall call them NIM 0, NIM 1, NIM
2 and NIM 3 for ease.
The rules for each are different although there is a certain degree of commonality.
NIM 0 (2-2 Nim)
1 There are two players.
2 Initial state: There 2 piles of matches, 2 matches in each pile.
3 Moves are made by alternate players.
4 Admissible transformations: Each player in a move selects a pile that
has at least one match and removes at least one match from this pile.
The player may take several matches, but only from one pile.
5 Terminal state: When both piles have no matches, there are no more moves and the game is over.
Outcome: Whoever takes the last match loses. The winner gets a dollar and the loser loses a dollar.
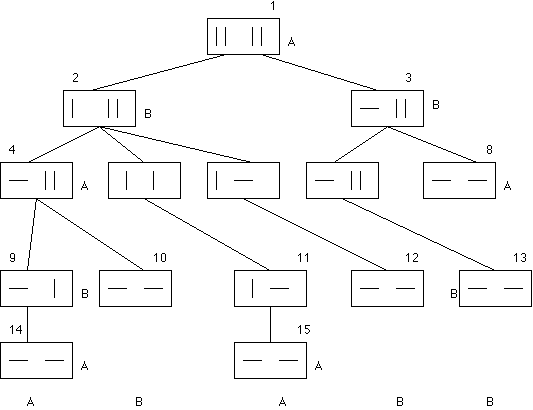
Analysis Method 1. (Using Extensive Form or Game Tree Method)
The term state is used here in a precise technical sense. In a game such as chess the same position can be reached in a varietyof different ways. In game theory we do not treat these positions as identical states. That is, a state is determined not only by the current position, but also by the unique history of play which led to that position.
The conventional way of representing a game is to use a game tree.
The boxes represent each state. The boxes occur at each point at which
a player has to make an admissible transformation. The interior of the
boxes represnt the piles of matches. The upper case letter by the box indicates
the player whose turn it is to play.
At states 14 and 15, A wins. At states 10, 12, and 13, B wins.
The diagram is simplified by taking advanatge of the symmetry. For instance, at the root, player has, in fact, four choices. The missing two choices really make no difference according to the rules of the game. A similar situation exists at state 5.
Notice that player A has three choices, as follows:
Choice A1: pick one match from the (2, 2) case and one match from the
(2,0) case.
Choice A2: pick one match from the (2, 2) case and two match from the
(2,0) case.
Choice A3: pick two matches from the (2, 2) case. (Notice that the
(2,0) case will not arise for player A.
Similarly, player B has six choices
Notice that player A has three choices, as follows:
Choice B1: If (2,0) take 2 matches, and if (2,1) take 1 from the smaller
pile.
Choice B2: If (2,0) take 2 matches, and if (2,1) take 1 from the larger
pile.
Choice B3: If (2,0) take 2 matches, and if (2,1) take 2 from the larger
pile.
Choice B4: If (2,0) take 1 match, and if (2,1) take 1 from the smaller
pile.
Choice B5: If (2,0) take 1 match, and if (2,1) take 1 from the larger
pile.
Choice B6: If (2,0) take 1 match, and if (2,1) take 2 from the larger
pile.
With the tree in place, we can do a bottoms up analysis - as follows.
At state 14 A wins, so at state 9 B has already lost, so at state 4 A will choose to go to 9, so state 4 is already a winning position for A, etc.
With this type of analysis, we discover A has lost the game before it starts, for a winning strategy for B is : If at state 2 go to sate 6, if at state 3 go to state 7.
Pruning
Counting the root as Level 1, we see that at Level 2, state 4, one of
A's strategies leads to sucess and the other leads to failure (i.e., B
wins). So we can prune the entire subtree emanating from state 4 and declare
A to be the winner at Node 4. Moving one step backwards, B can move from
state 2 to 6 to guarantee a win.
So if we ever come to state 4, B can force a win by moving to state
6.So at state 2, B is a winner. Moving back one level, to the root, A sees
that he cannot move to state 2. If he moves to state 3, that too would
make him lose. So the fate of A is sealed even before the game started!
Analysis Method 2 (Normal Form)
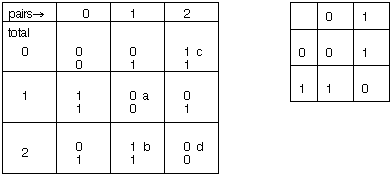
Another way of analyzing the game is to list all possible strategies for each player; for A as A1, A2, ... An and for B as B1, B2, ...Bm. Now we can imagine A playing startegy Ai and B playing Bj at each decision point and write the pay off matrix as (pij, -pij), this being a zero-sum game.
In NIM (2,2) if A plays A1 and B plays B1, let us see what happens.
According to A1 (look above, where A1 was defined), first A takes one match
leaving (2,1), then B takes one from the smaller pile, leaving (2,0). Strategy
A1 now tells A to pick one more match, leaving (1,0) and B must pick the
last match and so lose the game. So the payoff for this is (1, -1); A gets
$1 and B loses $1.The rest of the matrix can be filled like this.
| B1 | B2 | B3 | B4 | B5 | B6 | |
| A1 | 1 | 1 | -1 | 1 | 1 | -1 |
| A2 | -1 | 1 | -1 | -1 | 1 | -1 |
| A3 | 1 | 1 | 1 | -1 | -1 | -1 |
If we play A1 against A2, the sequence of play looks like this.
(2,2) --- A--(2,1) --B-- (1,1) --A-- (1, 0) --B-- (0, 0)
So A wins a gets a $1.
NIM 1
1 There are two players.
2 There is a single pile of matches.
3 Moves are made by alternate players.
4 Each player in a move can take up to half the number of matches in the pile.
5 Whoever takes the last match loses.
THEORY
There are safe and unsafe positions.
If a player leaves a pile with N matches where N is in the sequence
1, 3, 7, 15, 31, . . . , 2[n-1 ] for positive n then that player can force a win.
EXAMPLE
Suppose there are 53 matches initially then in binary
53 = 1 1 0 1 0 1
By removing the most significant digit and adding the least significant digit we get
0 1 0 1 0 1 +
0 0 0 0 0 1 =
0 1 0 1 1 0 which is 22.
Thus 22 matches must be withdrawn to leave a safe position and to enable the player to force a win.
NIM 2
1 There are two players.
2 There are several piles of matches.
3 Moves are made by alternate players.
4 Each player in a move can take any number of matches from a single pile.
5 Whoever takes the last match wins.
THEORY
Charles Bouton of Harvard University around 1900 showed that safe and unsafe positions also exist in this form of the game. The principle of the method lies in binary non-equivalence.
EXAMPLE
Suppose there are five piles initially and the number of matches in each pile are 1, 3, 5, 7, 11 and expressed in binary
0 0 0 1 1
0 0 1 1 3
0 1 0 1 5
0 1 1 1 7
1 0 1 1 11
1 0 1 1 != 2
In binary non-equivalence columns are added with no carry. Since the
result is non-zero the position is declared to be unsafe and it can be
made safe by removing a number of matches from one pile. To identify
the pile form the binary non-equivalence of the sum and each pile.
1 0001 3 0011 5 0101 7 0111 11 1011
1011 1011 1011 1011 1011
1010 1000 1110 1100 0000
as can be seen the answers in the first four cases are greater than the original piles and so the only
valid move is the last one which achieves a safe position.
NIM 3
1 There are two players.
2 There are several piles of matches.
3 Moves are made by alternate players.
4 Each player in a move can take any number of matches from an agreed number of piles, strictly less than the actual number of piles.
5 Whoever takes the last match wins.
THEORY
E H Moore has shown that safe and unsafe positions also exist in this
form of the game. The principle of the method lies in non-equivalence
but using P + 1 where P is the number of piles from which a player
can take matches in any turn.
EXAMPLE
Suppose there are five piles initially and the number of matches in
each pile are 1, 3, 5, 7, 11. A player can pick up matches from two plies.
The piles are expressed in ternary.
0 0 0 1 1
0 0 1 1 3
0 1 0 1 5
0 1 1 1 7
1 0 1 1 11
1 2 0 2 != 3
As the result is nonzero and the sum contains a digit 2 it indicates
that two piles need to be changed. In order to find which piles the attached
tables below are needed. The piles are taken in turn and paired off
and the digits are split into ordered pairs.
a b c d
TOTAL 1 2 0 2
SUM of 7&11 1 1 2 2
giving the ordered pairs (1,1) (2,1) (0,2) (2,2) and the result (0,0) (1,1) (1,1) and (0,0)
yielding 0110 and 0110 ie 6 in each case. The two piles 7 and 11 become 6 and 6.
AUTOMATIC GAME PLAYING
Mechanised game playing is studied partly for fun and partly as a model for real world events involving decision making. A game is a sequence of choices each choice being made from a number of discrete alternatives . Each sequence ends in an outcome and every outcome has a value in terms of the opening player. This can be a win +1 or a loss -1 and sometimes a draw 0. In other games the game can be scored for example Othello where there are 64 counters the scores could be registered as 63-1 or 33-31. The games we shall consider are called two-person games with perfect information and they are games played on boards or tables by two people who can both see all the board at all times and also the games do not involve chance as card games and backgammon do.
Game Representation
We can use directed graphs as shown for NIM in the diagram below or
trees as also shown. Trees are used if the path is needed and so for
the games we shall consider in this short course trees will be largely
used. Graphs can be of use as they involve less nodes and this is illustrated
in Grundy's game considered below.
Minimaxing
Every terminal node is given a value in terms of the opening player.
This leaves all the other nodes without a value. If we assume that each
player plays optimally and makes the best possible move on each occasion
then we can introduce the concept of minimaxing. Here the
opening player plays as though to maximise the value of the position
and the opponent minimises and tries to make the position worse for the
opening player. In any situation the opening player chooses the best
of all possible nodes to go to and this is maximising whereas the opponent
chooses the best position from the opponent's point of view which is
the worst from the opening player's. In this way the nodes above the
terminal ones can be scored provided it is known which player is in
play. Thus we can back up the values to all of the nodes and this is shown
in the tree diagram.
Foregone conclusion Theorem and a Fallacy
It would appear that from considering the tree that every game is a
foregone conclusion. If we assume that both players follow an optimal
strategy and that the value of the root node is the value of the game
then it can be seen at the outset who the winner will be. Unfortunately
for
some games such as Chess there are more moves than there are particles
in the universe 10[120] and so we are unable to follow this
prescribed course of action and find the optimal moves at each stage.
Strategies
It is possible that intelligence can be introduced by considering abstract
features that are known by experts or regular players to be useful
concepts, for example the parity in NIM and the use of binary non equivalence.
Turing initiated this discussion. The term lookahead can be
used to indicate the numberr of future possible moves analysed by either
player. Clearly there is a limit for most players and if the computer is
unrestricted no moves made be made because of resource difficulties
and so pruning at 3 ply is often introduced.
Heuristics and possible solutions
If the number of possible moves are restricted to 2 by the player in
play and one by the opponent then the terminal nodes are not true ones.
Those nodes that lie beyond the lookahead are termed dead positions
as they are beyond the radar screen and can only be observed by
changing the ground rules. The terminal nodes produced will have no
natural value and so an estimate of their value will be required to enable
the `best' move to be determined. This involves the development of an evaluation
function which makes use of the accumulated knowledge of the game culled
from books and experts.