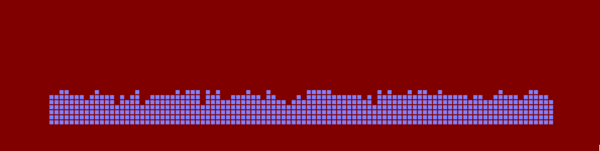
Hashing using two hash functions produces a distribution like this:
1/4: Introduction, change-making algorithm with and without
memoization.
change0.py, the original recursive program.
change1.py, the memoized version.
coinProof.pdf, my fourth version of the
brief proof that memoization
version uses 5n function calls.
Question to think about: Does the proof show that
the memoization version uses exactly 5n function calls, or does it give an
upper or lower bound?
Question to think about: Does the original version or the memoized
version use more memory?
1/6: Analysis of coin changing, merge sort, beginning of analysis
of merge sort.
Merge sort is in Section 2.3 in the book.
Question to think about: We decided we could not get a bound on
the running time by bounding the number of recursive calls.
Use the Master Method to bound the number of recursive calls. Do you
get the same asymptotic function as the one we got for the running time?
1/8: Proof by substitution, master
method. Introduction to randomized selection.
Proof by substitution is Section 4.1 and the Master Theorem is Section 4.3.
The sum we needed was
in Appendix A1. Randomized selection is in Section 9.2.
Here is Prof. Martel's handout on a
simplified version of the Master Theorem.
Question to think about: Our back-of-the envelope analysis assumed
that we split the problem into two equal-sized sub-problems at each iteration.
Do a back-of-the envelope analysis in which we assume (also incorrectly, but
a little more probably) that we split the the problem into two sub-problems
in which the size of the larger one is no more than three times the size
of the smaller one.
1/11: Analyzing randomized algorithms. The hiring problem.
Probability facts. Sections 5.1 and 5.2, probability review in
Appendix C.2.
Question to think about: Independence can be a tricky concept.
Does getting more information change the probability or not? A classic
example is the Monty Hall problem. I put three cards face down on the
table, and offer you a fabulous prize if you guess which
one is the ace of spades. You guess
some card. Then I turn over one of the two
cards that you didn't guess,
and show you that it isn't the ace of spades.
I tell you that if you want, you can change your guess. Should you?
1/13: Analysis of randomized selection. Finishing up Section 9.2.
1/15: Hashing, using chaining. How long can one chain get?
Sections 11.1 and 11.2.
Lecture notes on the length of the
longest chain in a hash table.
Question to think about: In Section 11.2 they prove that the
expected time to search for an item that is in the table is
O(1). This implies an upper bound on the length of the longest
chain; for instance, if the longest chain had length n then the
expected time to search for a random item would be O(n). What is the
best bound you can get on the length of the longest chain,
based on the fact that the expected time to search for a
random item is
O(1)?
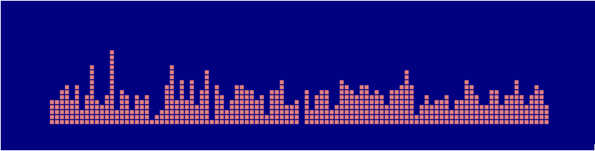
1/20: Finish up hashing. Demonstration of multiple-choice hashing.
Hashing using one hash function produces a distribution of chain lengths that looks like this:

Hashing using two hash functions produces a distribution like this:

1/22: Dynamic programming. Matrix sequence multiplication, Section 15.2.
Question to think about: We thought for a minute that we
maybe we could get an optimal algorithm by always choosing the smallest
matrix dimension in the seqence as the last dimension to multiply; for
instance, if we have 3x1 1x2 2x3, the smallest dimension is one and
the best choice would be 3x1 (1x2 2x3).
Give a sequence of three matrices such that choosing the smallest dimension
is not the best choice.
1/25: Properties of dynamic programming. A first cut at Longest Common
Subsequence. Sections 15.3 and the beginning of 15.4.
Question to think about: Consider the following recursive algorithm for
Uweighted Simple Longest Path from u to v, using the notation of Section 15.3.
For each vertex w, we consider solutions in which w is the last edge of the
Longest Path, so that the path ends in edge ew,v connecting w to
v. For each w adjacent to v, we remove v and all of its adjacent vertices
from the graph and then find the
Unweighted Simple Longest Path from u to w, recursively in the smaller graph,
producing a path Pw. Then we take the maximum
of length(Pw) + ew,v,
over all choices of w, as the length of the longest path.
What kind of an upper bound can you give for the
running time of this algorithm, using memoization?
1/27: Longest Common Subsequence. End of Section 15.4.
1/29: All-pairs shortest paths. Section 25.2.
2/1: Dijkstra's algorithm. Section 24.3. Here are some lecture notes. They include a question to think about. A suggestion about reading these notes: try to draw a picture for every idea, especially the Essential Lemma. Make yourself a "comic book" version of the proof as it goes along. You could also try making yourself a small example for every Lemma.
2/3: Midterm 1.
2/5: Minimum spanning tree. Chapter 23.
2/8: Maintaining connected components. Section 21.1 and 21.2.
Question to think about: We argued that maintaining the connected
components themseleves as rooted trees and keeping an auxillery array
to store the root of the tree containing each vertex allowed us to
implement Kruskal's algorithm in O(m lg n) time. Explain exactly how
to merge together the two rooted trees when two components are connected
by a new edge.
2/10: Amortized analysis using a potential function. Sections 17.3 and 17.4.
Question to think about: Check that deletions always have an amortized
cost of at most three.
2/12: Disjoint sets data structure, the rank function, and
path compression.
Here are some Prof. Trevisan's lecture notes,
from Berkeley, giving the simpler proof that we will cover.
2/15: Holdiay.
2/17: Finish disjoint sets analysis.
2/19: Huffman encoding. Section 16.3.
2/22: More Huffman encoding, introduction to entropy.
2/24: Sorting lower bound, begin entropy lower bound. Section 8.1.
2/26: The entropy lower bound. Lecture notes to appear here soon.
3/1: Intro to NP-completeness. Sections 34.1 and 34.3.
3/3: Midterm 2.
3/5: Checkability and NP-completeness. Section 34.2. 3/8: NP-complete problems. Section 34.5.