A data-driven approach to characterizing wine regionality: Applications to Malbec wines

|
Unraveling the regional specificities of Malbec wines from Argentina and Northern California
Hsieh Fushing, Olivia Lee, Constantin Heitkamp, Hildegarde Heymann, Susan E. Ebeler, Roger B. Boulton, Patrice Koehl
In any scientific settings, experiments are devices that are used to provide insight into the relationships between the features that control a system and the observations that are made on this system. Analyzing those relationships between features and observations for the set of objects under study can be complicated by possible additional relationships between the features themselves.
In this paper, we propose a new approach for performing the analysis of an experiment that relies on these relationships instead of trying to circumvent them. This new approach follows two steps. We first cluster the objects of the experiment using each feature independently. We then assign a distance between two features to be the mutual entropy of the clustering results they generate. The set of features is then clustered using this distance measure. The result of this clustering is a set of sub-groups of features, such that two features in the same group carry similar, i.e. synergetic information with respect to the objects of the experiment. The objects are then analyzed separately on the different sub groups of features, using the recently proposed Data Mechanics approach.
We have used this method to analyze the similarities and differences between Malbec wines from Argentina and California, as well as the similarities and differences between sub-regions of those two main wine producing countries. We report detection of groups of features that characterize the origins of the different wines included in the study.
All datas for this study:
|
Data Cloud Geometry: generating an ultrametric distance measure on data

|
DCG++: A data-driven metric for geometric pattern recognition
Jiahui Guan, Hsieh Fushing, Patrice Koehl
Clustering large and complex data sets whose partitions may adopt arbitrary shapes remains a difficult challenge.
Part of this challenge comes from the difficulty in defining a similarity measure between the data points that
captures the underlying geometry of those data points.
In this project, we propose an algorithm, DCG++ that generates such a similarity measure that is data-driven and ultrametric.
DCG++ uses Markov Chain Random Walks to capture the intrinsic geometry of data, scans possible scales, and combines all this information using a simple procedure that is shown to generate an ultrametric.
We validate the effectiveness of this similarity measure on synthetic data with complex geometry, on a real-world data set as well as on an image segmentation problem.
The experimental results show a significant improvement on performance with the DCG-based ultrametric compared to using an empirical distance measure.
All programs for this study:
- DCG.tgz: Compressed archive for source code under LGPL license
- README: simple README for compiling and running the program
|
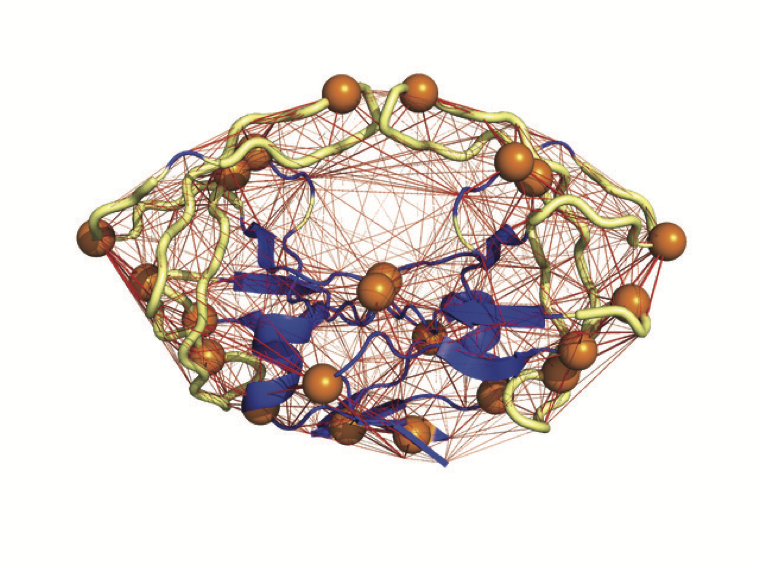
Parameterizing Elastic Network Models to Capture the Dynamics of Proteins
|
FitNMA: parameterizing elastic networks of proteins
Patrice Koehl, Henri Orland, Marc Delarue
Coarse-grained normal mode analyses of a protein rely on the idea that the geometry of its structure contains enough information for computing its fluctuations around its equilibrium conformation, chosen to be the crystal structure.
This geometry is captured in the form of an elastic network (EN), i.e. a network of edges between its residues.
A spring is associated with each edge.
The normal modes of the protein are then identified with the normal modes of its EN.
Different approaches have been proposed to construct ENs, focusing on their geometries, i.e. the choice of the edges that are comprised of, as well as on their parameterizations, i.e. the choice of the force constants associated with those edges. We have analyzed both facets of EN.
We study first different geometric models for constructing the EN.
We compare cutoff-based ENs, whose edges have lengths that are smaller than a cutoff distance, with Delaunay-based ENs and find that the latter provide better representation of the geometry of protein structures, in particular in their abilities to capture long range interactions.
We then derive an analytical method for the parameterization of the EN
such that its dynamics leads to atomic fluctuations that are in agreement with experimental B-factors.
To reduce the risk of overfitting in this procedure, we attach a parameter (referred to as flexibility constant) to each atom instead of to each edge in the EN.
We express the parameterization as a non linear optimization problem whose parameters are the variables associated with rigid motions and the atomic flexibility constants associated with internal motions.
We derive analytical expressions for the function that computes the atomic B-factors from those parameters as well as for its derivatives with respect to those parameters.
We show that the parameterization leads to improved ENs, as it defines dynamics for those ENs that is closer to MD simulations than for ENs with uniform force constants, and reduces the number of normal modes needed to reproduce functional conformational changes.
All programs for this study:
- FitNMA.tgz: Compressed archive for source code under LGPL license
- README: simple README for compiling and running the program
|
Map2Sphere: parametrizing a genus zero surface onto the sphere

|
Map2Sphere: Parameterizing genus-zero triangulated surface onto the sphere
Patrice Koehl, Joel Hass
Parametrization is the process of computing a correspondence between a triangulated surface and a domain in a canonical space. We are particularly interested in genus-zero surfaces, in which case the canonical space is the sphere, and in conformal maps, which preserve angles between the source surface and the sphere. We have implemented
different methods for computing such a parameterization, from intrinsic methods (i.e. methods based on edge lengths), such as Ricci flow and Yamabe flow, to extrinsic methods (methods that directly work on the Cartesian coordinates), such as Tutte embeddings, conformalized mean curvature flow, and Willmore flow. Finally, we have implemented normalization techniques, such as applying a Mobius transform to arrange the vertices on the sphere such that their center of gravity sits at the center of the sphere, as well as a quasi conformal Beltrami flow to improve
the conformality of an existing map.
All programs for this study:
- Map2Sphere.tgz: Compressed archive for source code under LGPL license
- README: simple README for compiling and running the program
|
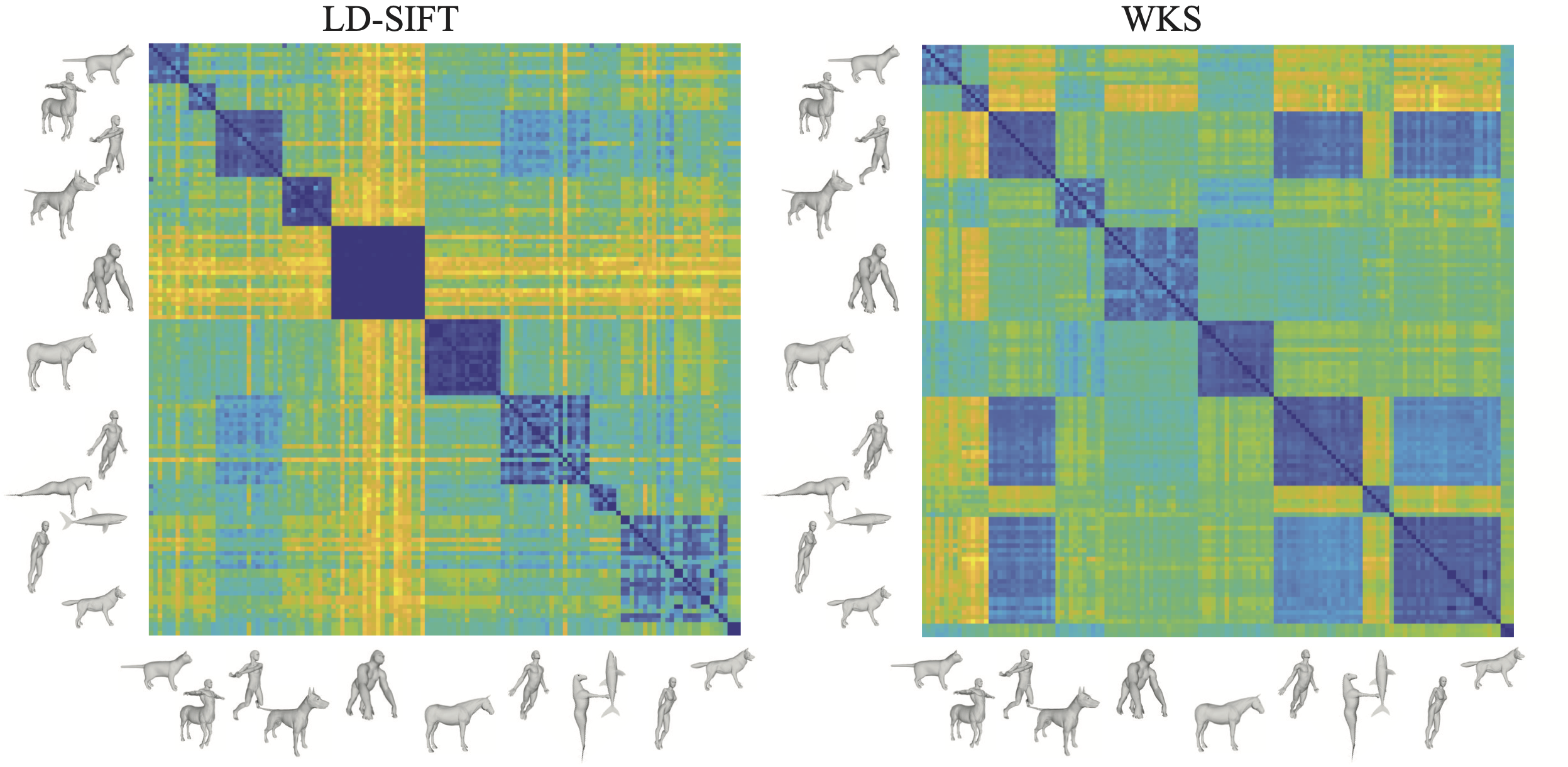
Comp3DShapes: A Physicist's view on Partial Shape Comparison
|
Comp3DShapes: A Physicist's view on Partial Shape Comparison
Patrice Koehl, Henri Orland
Place holder...
All programs and data for this study:
|
Elastic Network Models, Rigidity, and Protein Dynamics

|
Elastic Network Models, Rigidity, and Protein Dynamics
Patrice Koehl, Joel Maier, Kelin Xia
Place holder...
All programs and data for this study:
- ProteinNM: Compressed zip archive for source code under LGPL license
- README: simple README for compiling and running the program
- Bastolla: While all data come from the PDB, for convenience we provide all PDB files used in the study
|
|





