Modeling and Data Analysis in Life Sciences: 2017

Project 2: Protein Structure Geometry

Handouts

Volume of a protein:

Word document (click to download)
or
PDF document (click to download)

Additional information: protein.crd

Measuring protein structures

A common concrete model for proteins is to represent them as a union of balls, in which each ball corresponds to an atom. Properties of a protein are then expressed in terms of properties of the union. For example, the interaction of the protein with its environment is quantified through the surface area and/or volume of the union of balls, and its potential active sites are detected as cavities.

How do we compute geometric properties of a protein, represented as a union of ball? This is by far not an easy problem! Analytical solutions to that problem exist, but they are not easy to implement. Here we will use numerical methods to solve this problem that are surprisingly accurate and easy to implement. These methods are based on the scientific computing technique called "Monte Carlo integration".

Monte Carlo Techniques:

Let us assume we want to compute the integral $I$ of a function $f$ over a multidimensional volume $V$. Suppose that we have picked $N$ random points, uniformly distributed in a multidimensional volume $V$. Call them $x_1,\ldots,x_N$. The basic theorem of Monte Carlo integration estimates the integral $I$ as: $$\int f dV \approx V \langle f \rangle \pm V \sqrt{ \frac{ \langle f^2\rangle - \langle f \rangle^2}{N}}$$

Here the brackets denote taking the arithmetic mean over the N sample points,

$$\langle f \rangle = \frac{1}{N} \sum_{i=1}^N f(x_i) \quad \quad \quad \langle f^2 \rangle = \frac{1}{N} \sum_{i=1}^N f^2(x_i)$$

The "plus-or-minus" term is a one standard deviation error estimate for the integral. To understand how it can be applied to computing a volume, lest us look at a simple toy problem in 2D, where we want to compute the surface area of two overlapping disks.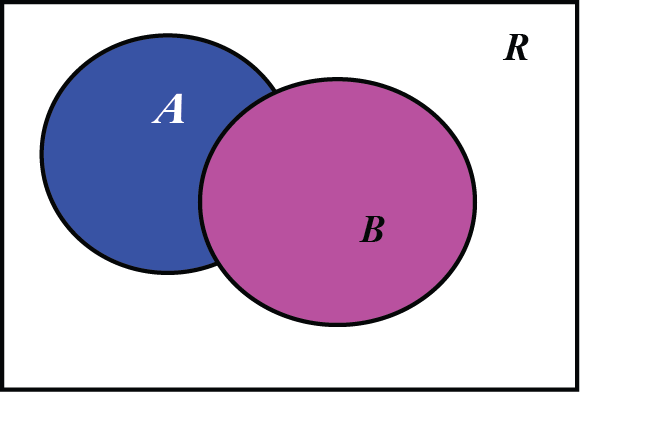

We define the function $f$ as:

For all $x$ in $R$, $f(x) = 1$ if $x \in A\cup B$, and $f(x)=0$ otherwise.

To compute the surface area covered by the two disks A and B, which we denote $S(A\cup B)$, we use the following algorithm:

Initialize $S=0$ and $S_2 = 0$
Initialize number of random points N
For $i=1:N$
- Position $x_i$ at random in box $R$
- Compute $f(x_i)$: if the distance from $x_i$ to the center of $A$ is smaller than the radius of $A$ or if the distance from $x_i$ to the center of $B$ is smaller than the radius of $B$, then $f(x_i)=1$; in all other cases, $f(x_i)=0$
- Update the sums: $S=S+f(x_i)$; $S_2 = S_2+f(x_i)^2$
Compute means: $$\langle f \rangle = \frac{S}{N} \quad \quad \langle f^2 \rangle = \frac{S_2}{N}$$
Compute surface area: $$S(A\cup B) = S(R)\langle f \rangle$$ where $S(R)$ is the surface area of the rectangular box $R$.
Compute the one standard deviation error estimate: $$SD = \sqrt{ \frac{ \langle f^2\rangle - \langle f \rangle^2}{N}}$$

This algorithm can be generalized to any number of disks, and any dimensions.

Problem:

Adapt the algorithm above to the problem of computing the total volume of a union of balls.
Write a small program implementing this algorithm.
Apply this program on the test case protein.crd. Show how the estimate of the volume changes as you vary N, the number of points you consider.
(Using an analytical method, I found the volume of this union of balls to be 35490.34 Å3)

Please provide both the source code of the program you wrote, and a report describing the results.