Modeling and Data Analysis in Life Sciences: 2017

Lab 6: Population dynamics via cellular automata

Handouts

Cellular automata

Cellular automata provide a simplified way of modeling physical, biological or social phenomena. In a CA model the "universe" is divided up into small cells. Each cell can take any one of a finite number of states (such as. live or dead). A single generation is determined by assigning a state to each of the cells. Then a strict (and often quite simple) set of rules is used to determine how a given generation evolves into the next one. The model then consists of repeated applications of the rules to obtain each successive generation from the previous one. In principle this iteration can go on forever; in computer implementations however, it goes on for a finite (possibly quite large) number of generations. There is much interest in CA models among mathematicians and applied scientists such as ecologists or biologists.

Let us consider a flat square universe, divided up into an \(N \times N\) array of small cells, denoted \((i, j)\), for \(i, j = 1, \ldots, N\). The states of these cells may be represented as the elements \(A(i, j)\) of a matrix \(A\). The immediate neighbors of cell \((i,j)\) are defined to be those cells that touch it (excluding cell \((i,j)\) itself). So an interior cell \((i,j)\) (where \(i = 2,\ldots,n-1\) and \(j = 2,\ldots,n-1\)) has immediate neighbors \((i-1,j-1), (i-1,j), (i-1,j+1), (i,j-1), (i,j+1), (i+1,j-1), (i+1,j)\), and \((i+1,j+1)\):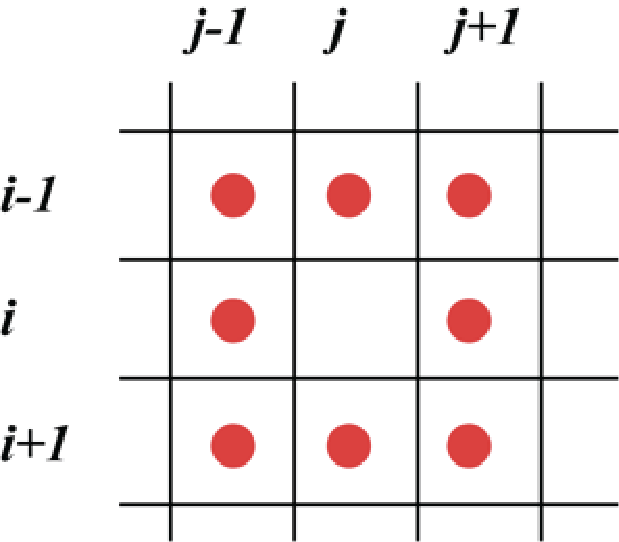

In this universe, each cell can occupy only two states (alive or dead, but other interpretations are possible). We represent these by setting \(A(i,j) = 1\) when the cell \((i,j)\) is alive and \(A(i, j) = 0\) when it is dead.

Each generation is determined from the previous one according to (majority scheme):

• A live cell dies in the next generation if more than 4 of its immediate neighbors at the present generation are dead; otherwise it stays alive.
• A dead cell comes to life in the next generation if more than 4 of its immediate neighbors at the present generation are alive; otherwise it stays dead.

To apply these rules consistently, we need to define the states of the cells that lie just outside the boundary of the universe (remember that our universe is finite, of size \(N \times N\)). For example, we shall say that all cells outside the boundary of our universe are assumed to be dead.

The purpose of this project is to generate a model for this simple automaton, i.e. a finite number of generations, starting from a random initial organization of the universe.

1. Define initial status of the universe
   
   

   For a given value of \(N\), the code segment below initialize a matrix \(B\) of size \(N \times N\) to 0, select 10% of its cells at random, and set these cells to 1:

   
   B = zeros(N,N);
   %
   nval = numel(B);
   R = randperm(nval);
   n10 = floor(nval*0.1);
   B(R(1:n10)) = 1;
   
   

   Complete and modify this program such that:

   • It allows for any initial percentage P of cell that are alive
   • It embeds the matrix \(B\) into a larger matrix \(A\) of size \((N+2) \times (N+2)\), such that \(B\) covers the rows 2 to \(N+1\) and the columns 2 to \(N+1\), with the first and last rows of \(A\) and the first and last columns of \(A\) set to 0 (this corresponds to adding the fist layer outside the boundary of \(B\)).


2. Visualize the initial state of the automaton
   
   

   The easiest way to display the matrix \(A\) is to generate a black and white image of \(A\) that is then displayed in a graphic window. The code fragment below does that:

   
   C=255*uint8(A);
   h=imshow(C,'InitialMag','fit');
   
   

   check the functions uint8 and imshow to understand what this code does.

   The figure below shows an example for \(N=10\), with 10% of the cells set alive (shown in white).

   


3. Update the automaton
   Starting from a conformation A of the universe, we apply the majority scheme defined above with these five steps:
   1. Define two intermediate matrices ANEW and L of the same size of A, with all elements set to 0:
      

      
      ANEW = zeros(N+2,N+2);
      L = ANEW;
      
      

   2. For \(i, j = 2, \ldots, n + 1\), compute the number of live cells that are nearest neighbors of cell \((i, j)\). Put it in the matrix entry \(L(i,j)\).
   3. Initialize ANEW to A. Then change some entries of ANEW as appropriate:
      

      
      For i=2:n+1 and j=2:n+1, 
       	if A(i,j) = 1 and L(i,j) < 4 
      		ANEW(i,j) = 0; 
      	end
      	if A(i,j) = 0 and L(i,j) > 4 
      		ANEW(i,j) = 1;
      	end
      end
      
      

   4. Set \(A\) to \(ANEW\)
   5. Visualize the new matrix A:
      

      
      C = 255*uint8(A);
      h.CData = C;
      drawnow;
      
      

      Implement this pseudo code into Matlab. Modify the corresponding code so that it repeats this procedure over M generations.



4. Running the program
   
   

   Put together all code segments corresponding to the three sections above, and test your program for different values of N and P (set M=20). Show an image of the final state of the universe (with M=20) for the three cases:

   • N = 100, P = 10
   • N = 100, P = 50
   • N = 100, P = 90