AIX008: Introduction to Data Science: Summer 2022

Application of kNN for regressions

The following hands-on exercises were designed to teach you step by step how to build k-NN models based on given data, assess and select the best of thse models based on training data, and finally to use this model to predict values on a test dataset. We use the "advertising" dataset (available locally at advertising.csv, which contains information on 200 markets. For each market, we know the amount that was spent for advertisement of a product on TV, radio, and in newspaper, and the corresponding sales amount of the product.

The questions we would like to answer are:

Which of the three methods of advertisement is a better predictor of sales?
Can we predict the sales from TV advertisement alone using a kNN model?
Do we get better predictions if we use data from all three methods of advertisement?

The advertising data set

We first examine the relationships between TV, Radio, newspaper advertisement, and sales, separately. Here is a small Matlab script that reads in the dataset, and illustrates those relationships as scatter plots: advertising.m


>> ad=readtable("advertising.csv");
>> ad=rmmissing(ad);
>> figure
>> subplot(1,3,1)
>> plot(ad.TV, ad.Sales,'or','lineWidth',1.5)
>> xlabel('TV advertising (in $1000)')
>> ylabel('Sales (in $1000)')
>> subplot(1,3,2)
>> plot(ad.Radio, ad.Sales,'or','lineWidth',1.5)
>> ylabel('Sales (in $1000)')
>> xlabel('Radio advertising (in $1000)')
>> subplot(1,3,3)
>> plot(ad.Newspaper, ad.Sales,'or','lineWidth',1.5)
>> ylabel('Sales (in $1000)')
>> xlabel('Newspaper advertising (in $1000)')

And here are the plots: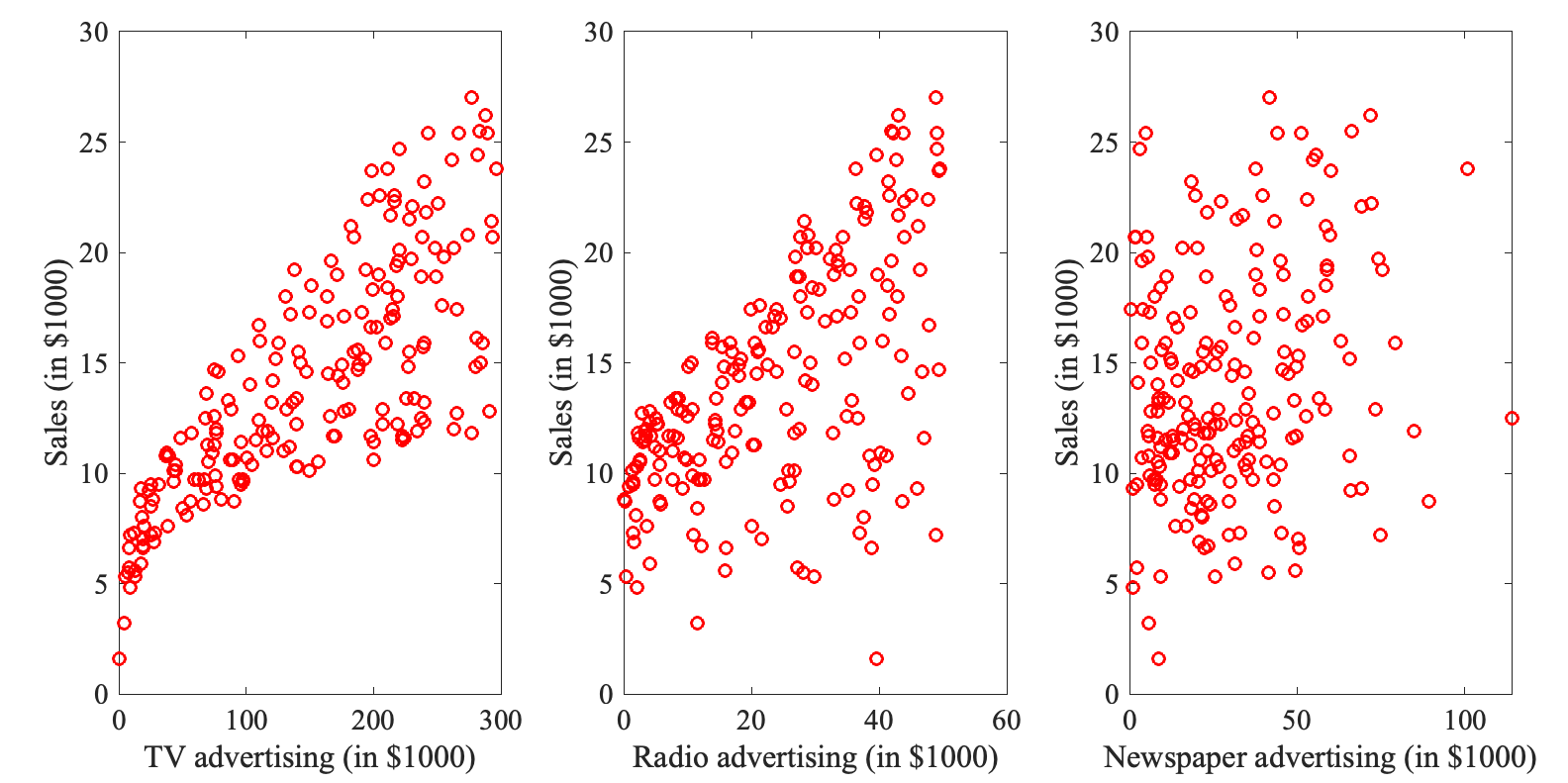

Clearly, TV advertising correlates best with sales. We will then build kNN models based on TV advertisement alone.

A kNN model to predict sales based on TV advertising

Our tast is to build kNN models from TV advertising data, choose the best of these models based on a training set, and finally use this model on a test set. To do this, I have divided the advertising dataset into three sets:

A DATA set: ad_data.csv
A Training set: ad_training.csv
A Test set: ad_test.csv

Here is a small Matlab script that reads in these three datasets and shows the different points on a scatter plot TV / Sales in different colors..read_sets.m

>> data=readtable('ad_data.csv');
>> train=readtable('ad_training.csv');
>> test=readtable('ad_test.csv');
>> data_val=[data.TV data.Sales];
>> train_val=[train.TV train.Sales];
>> test_val=[test.TV test.Sales];
>> figure
>> plot(data_val(:,1),data_val(:,2),'ok','LineWidth',0.5)
>> hold on
>> plot(train_val(:,1),train_val(:,2),'ob','LineWidth',1.5)
>> plot(test_val(:,1),test_val(:,2),'or','LineWidth',1.5)
>> ylabel('Sales (in $1000)')
>> xlabel('TV advertising (in $1000)')
>> legend('Data','Train','Test')

And here is the plot: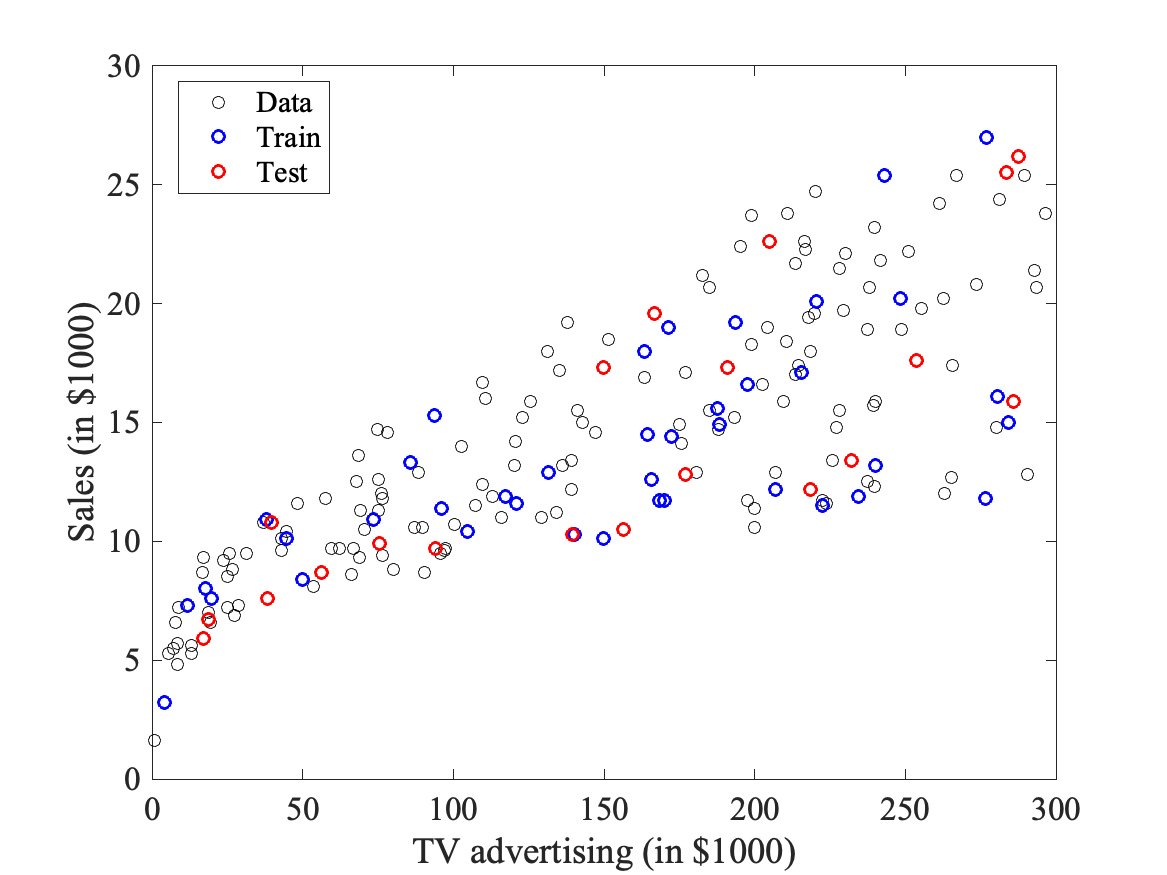

The following Matlab script build a 1-NN model from the Data set and uses the training set to evaluate it using RMSE. It also plots the real values and predicted values for the training set: knn1.m


>> ntrain=max(size(train_val)); % number of training data
>> rmse=0;                      % Initialize RMSE to 0
>> for i = 1:ntrain             % For each training point
val = train_val(i,1);           % TV value for this point
dist=abs(data_val(:,1)-val);    % Computes distance to all points in DATA
[t,idx]=sort(dist);             % Sort these distances
y=data_val(idx,2);              % Order the SALES value in DATA set accordingly
y_predict(i) = y(1);            % This is a 1-NN: pick the first value
rmse = rmse + (train_val(i,2)-y(1)).^2;   % Update RMSE: add square of differences
end                             % end loop
>> rmse = sqrt(rmse/ntrain);    % Compute RMSE
>> figure
>> plot(train_val(:,2),y_predict,'or','LineWidth',1.5);
>> xlabel('Real value for sales of training dataset')
>> ylabel('Predicted value for sales of training dataset')
>> title("RMSE = " + rmse);

And here is the plot: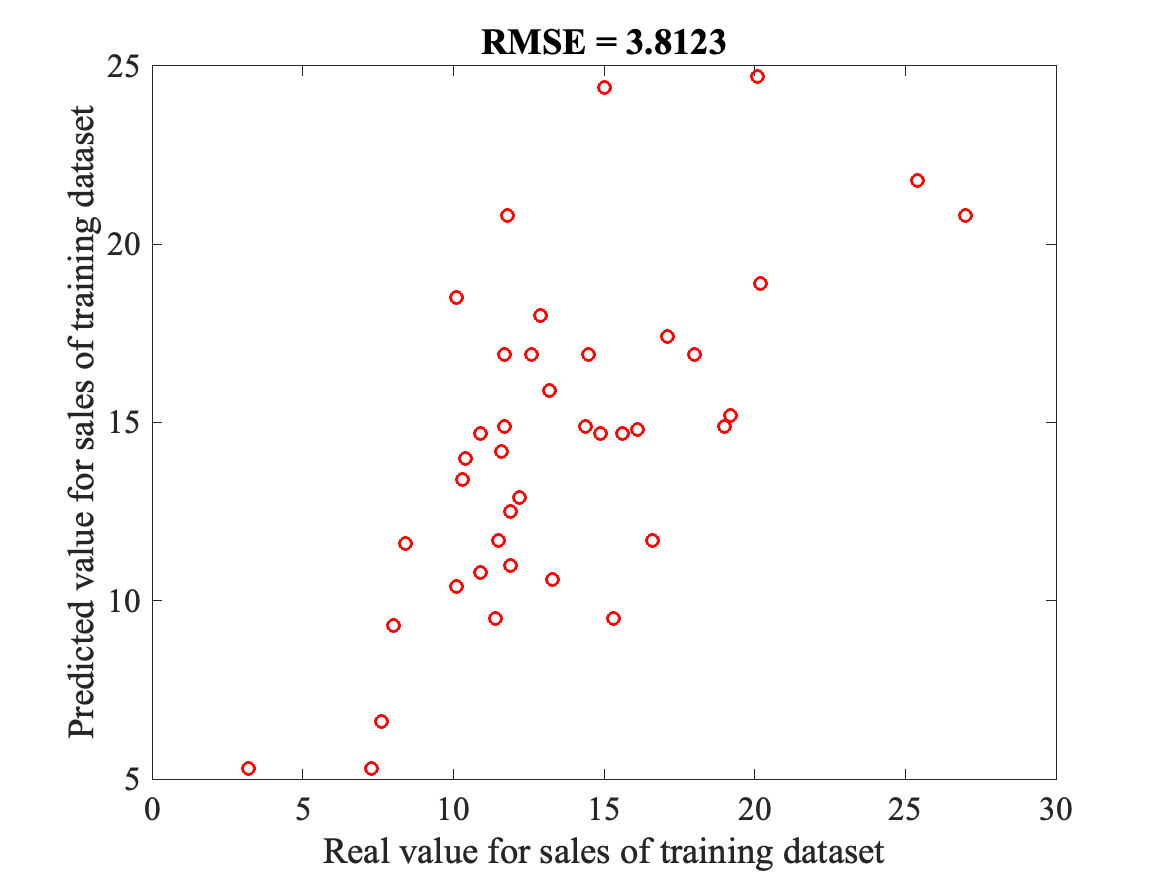

This shows that the 1-NN is "reasonable", with a RMSE of 3.81.

After adapting this script, you will:

Repeat this analysis over the training set, build k-NN models for k = 2, 3, ...., 10
Plot the corresponding RMSE values against k. Pick the best k, k_best
Build a k-best-NN model on the DATA set, and test it on the TEST set. What is the corresponding RMSE?

A kNN model to predict sales based on all forms of advertising

The analysis you have performed above was based on TV advertising only. Repeat the whole analysis, using now all three forms of advertising. I provide the corresponding script for the 1-NN knn1_all.m:


>> data_all = [data.TV data.Radio data.Newspaper data.Sales];
>> train_all = [train.TV train.Radio train.Newspaper train.Sales];
>> ntrain=max(size(train_all));
>> ndata=max(size(data_all));
>> for i = 1:ntrain
val=train_all(i,1:3);
for j = 1:ndata
dist(j) = norm(data_all(j,1:3)-val);
end
[t,idx]=sort(dist);
y=data_all(idx,4);
y_predict(i) = y(1);
rmse=rmse+(train_all(i,4)-y(1)).^2;
end
>> rmse=sqrt(rmse/ntrain);
>> figure
>> plot(train_all(:,4),y_predict,'or','LineWidth',1.5)
>> xlabel('Real value for sales of training dataset')
>> ylabel('Predicted value for sales of training dataset')
>> title("RMSE = " + rmse);

And the corresponding plot: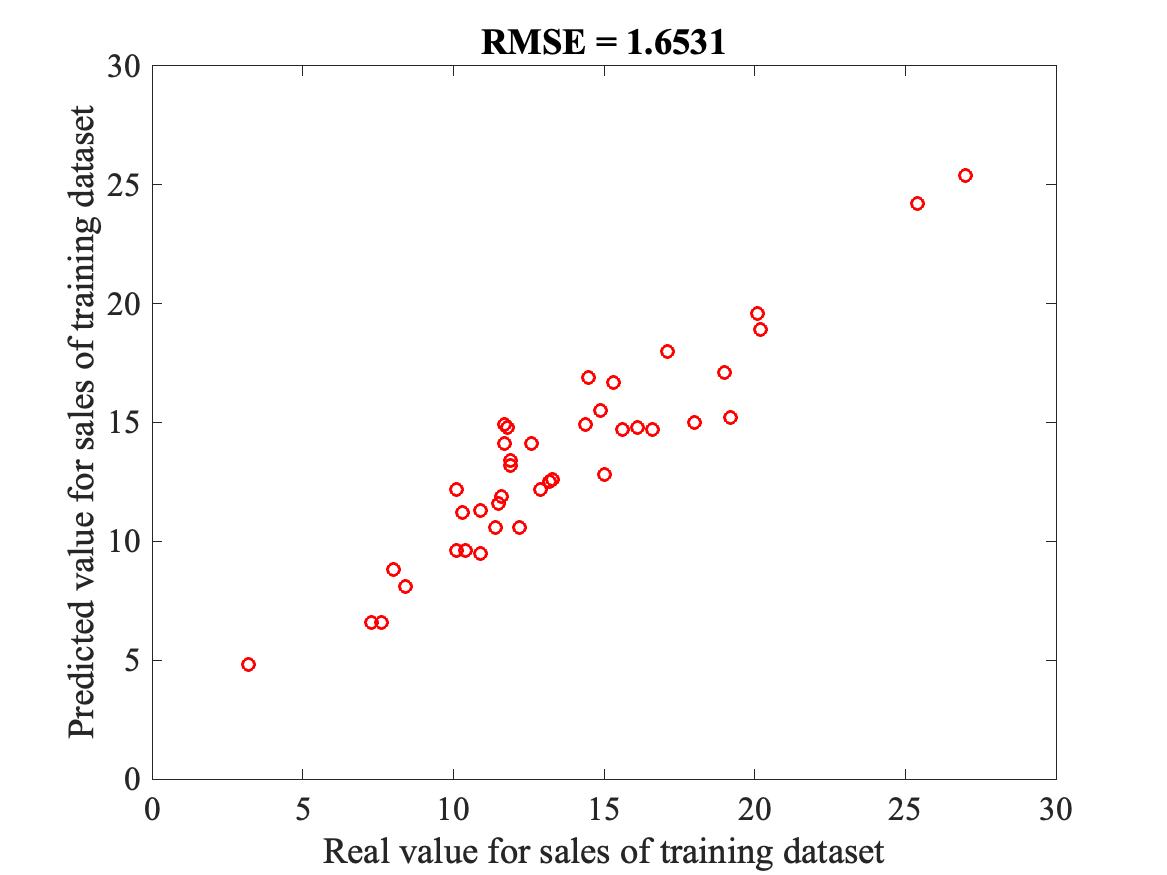

This shows that the 1-NN based on ALL data is "reasonable" and better than the 1-NN based on TV advertisement only, with a RMSE of 1.65.

After adapting this script, you will:

Repeat this analysis over the training set, build k-NN models for k = 2, 3, ...., 10
Plot the corresponding RMSE values against k. Pick the best k, k_best
Build a k-best-NN model on the DATA set, and test it on the TEST set. What is the corresponding RMSE?